Ứng dụng của công thức lượng giác vào thực tế
Công thức lượng giác có nhiều dạng bài tập khác nhau chắc chắn đã gây không ít khó khăn cho các bạn học sinh đặc biệt là về phần bài toán thực tế.
Mục lục bài viết
Trong các bài kiểm tra không thể thiếu phần bài tập thực tế, đặc biệt là môn toán. Do đó, các bài toán thực tế lượng giác dần trở thành nỗi lo của các bạn học sinh khi muốn đạt điểm cao.
Vậy nên, Examon đã tổng hợp lại phương pháp giải, ví dụ và bài tập về phần công thức lượng giác để các bạn học sinh dễ dàng hơn trong quá trình giải bài tập của mình.

1. Phương pháp giải
Để giải được các bài toán thực tế, ta cần linh hoạt sử dụng các công thức lượng giác đã học (công thức cộng lượng giác, công thức nhân đôi, công thức biến đổi tích thành tổng, tổng thành tích), các giá trị lượng giác đặc biệt và các hằng đẳng thức lượng giác.
2. Ví dụ minh họa
2.1 Ví dụ 1
Một thiết bị trễ kĩ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần \(\mathrm{f}_{1}(\mathrm{t})=5 \operatorname{sint}\) và phát lại được nốt thuần \(\mathrm{f}_{2}(\mathrm{t})=5 \cos t\) thì âm kết hợp là \(\mathrm{f}(\mathrm{t})=\mathrm{f}_{1}(\mathrm{t})+\mathrm{f}_{2}(\mathrm{t})\), trong đó \(\mathrm{t}\) là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng \(f(t)=k \sin (t+\varphi)\), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm \(\mathrm{k}\) và pha ban đầu \(\mathrm{j}(-\pi \leq \varphi \leq \pi)\) của sóng âm.
Lời giải
Ta có:
\(\begin{array}{l}f(t)=f_{1}(t)+f_{2}(t) \\ =5 \sin t+5 \cos t \\ =5(\sin t+\cos t) \\ =5 \sqrt{2}\left(\frac{\sqrt{2}}{2} \sin t+\frac{\sqrt{2}}{2} \cos t\right) \\ =5 \sqrt{2}\left(\sin t \cos \frac{\pi}{4}+\cos t \sin \frac{\pi}{4}\right) \\ =5 \sqrt{2} \sin \left(t+\frac{\pi}{4}\right) .\end{array}\)
Vậy \(k=5 \sqrt{2}\) và \(\varphi=\frac{\pi}{4}\).
2.2 Ví dụ 2
Trong Vật lí, phương trình tổng quát của một vật dao động điều hòa cho bởi công thức \(x(t)=A \cos (\omega t+\varphi)\), trong đó \(t\) là thời điểm (tính bằng giây), \(x(t)\) là li độ của vật tại thời điểm \(t, A\) là biên độ dao động \((A\gt 0)\) và \(\varphi \in[-\pi ; \pi]\) là pha ban đầu của dao động. Xét hai dao động điều hòa có phương trình \(x_{1}(t)=2 \cos \left(\frac{\pi}{3} t+\frac{\pi}{6}\right)(\mathrm{cm})\), \(x_{2}(t)=2 \cos \left(\frac{\pi}{3} t-\frac{\pi}{3}\right)(\mathrm{cm})\). Tìm dao động tổng hợp \(\mathrm{x}(\mathrm{t})=\mathrm{x}_{1}(\mathrm{t})+\mathrm{x}_{2}(\mathrm{t})\) và sử dụng công thức biến đổi tổng thành tích để tìm biên độ và pha ban đầu của dao động tổng hợp này.
Lời giải
Có \(x(t)=x_{1}(t)+x_{2}(t)\) nên
\[\begin{array}{l}x(t)=2 \cos \left(\frac{\pi}{3} t+\frac{\pi}{6}\right)+2 \cos \left(\frac{\pi}{3} t-\frac{\pi}{3}\right) \\=2\left[\cos \left(\frac{\pi}{3} t+\frac{\pi}{6}\right)+\cos \left(\frac{\pi}{3} t-\frac{\pi}{3}\right)\right] \\=4\left[\cos \frac{\left(\frac{\pi}{3} t+\frac{\pi}{6}\right)+\left(\frac{\pi}{3} t-\frac{\pi}{3}\right)}{2} \cos \frac{\left(\frac{\pi}{3} t+\frac{\pi}{6}\right)-\left(\frac{\pi}{3} t-\frac{\pi}{3}\right)}{2}\right] \\=4\left[\cos \left(\frac{\pi}{3} t-\frac{\pi}{12}\right) \cos \frac{\pi}{4}\right] \\=2 \sqrt{2} \cos \left(\frac{\pi}{3} t-\frac{\pi}{12}\right) .\end{array}\]Vậy \(A=2 \sqrt{2}\) và \(\varphi=-\frac{\pi}{12}\).
3. Bài tập tự luyện
3.1 Bài tập 1:
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là \(x_{1}=6 \cos 100 \pi t(\mathrm{~mm})\) và \(x_{2}=6 \sin 100 \pi t(\mathrm{~mm})\), (t tính bằng giây). Tính li độ của vật tại thời điểm t = 0,25 giây.
A. 6 ;
B. -6 ;
C. \(12 ;\)
D. -12 .
3.2 Bài tập 2:
Cho hai dao động điều hòa cùng phương có phương trình lần lượt là \(x_{1}=\) \(5 \cos (100 \pi t+\pi)(\mathrm{cm})\) và \(x_{2}=5 \cos \left(100 \pi t-\frac{\pi}{2}\right)(\mathrm{cm})\). Phương trình dao động tổng hợp của hai dao động trên là
A. \(5 \sqrt{2} \cos \left(100 \pi t+\frac{3 \pi}{4}\right)(\mathrm{cm})\)
B. \(5 \sqrt{2} \cos \left(100 \pi t-\frac{3 \pi}{4}\right)(\mathrm{cm})\)
C. \(10 \cos \left(100 \pi t-\frac{3 \pi}{4}\right)(\mathrm{cm})\)
D. \(10 \cos \left(100 \pi t+\frac{3 \pi}{4}\right)(\mathrm{cm})\).
3.3 Bài tập 3:
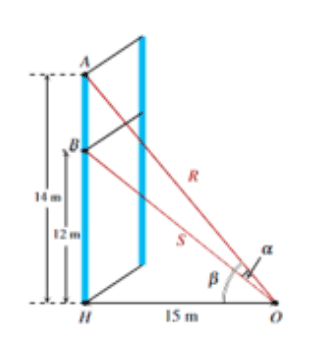
Một sợi cáp \(R\) được gắn vào một cột thẳng đứng ở vị trí cách mặt đất \(14 \mathrm{~m}\). Một sợi cáp \(S\) khác cũng được gắn vào cột đó ở vị trí cách mặt đất \(12 \mathrm{~m}\). Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột \(15 \mathrm{~m}\). Tính tana (a là góc giữa hai sợi dây cáp trên).
A. \(\frac{14}{15}\);
B. \(\frac{12}{15}\);
C. \(\frac{10}{131}\) ;
D. \(\frac{130}{19}\).
3.4 Bài tập 4:
Một vật thực hiện đồng thời hai dao động điều hòa có phương trình \(x_{1}(t)=2 \sqrt{3} \sin \left(4 \pi t+\frac{\pi}{6}\right)\) và \(x_{2}(t)=2 \cos \left(4 \pi t+\frac{\pi}{6}\right)\). Biết rằng phương trình dao động tổng hợp của vật đó \(x(t)=x_{1}(t)+x_{2}(t)\) viết được dưới dạng \(x(t)=A \cos (\omega t+\) \(\varphi)\). Xác định \(\omega\).
A. \(\frac{\pi}{6}\)
B. \(-\frac{\pi}{6} ;\)
C. \(4 \pi ;\)
D. \(4 \pi t\).

4. Tiến bước cùng Examon
Trên đây Examon đã tổng hợp đầy đủ từ phương pháp giải đến các bài tập về bài toán thực tế phần công thức lượng giác. Hy vọng rằng bài viết sẽ giúp cho các bạn học sinh có thể học tốt môn toán và không con lo về phần lượng giác nữa. Đồng hành cùng Examon để đạt kết quả cao trong học tập.
PHƯƠNG PHÁP HỌC HIỆU QUẢ với EXAMON
Có bao giờ bạn tự hỏi tại điểm kiểm tra của mình thấp không?
Mình cũng từng bị như vậy và luôn hỏi tại sao suốt 1 thời gian dài và giờ mình đã tìm ra câu trả lời “Đó chính là phương pháp học không đúng".
Để học hiệu quả bạn nên làm những gì?
Đầu tiên nên thiết kế lộ trình bứt phá điểm số của mình như sau:
Bước 1: Bạn cần có 1 cuốn sổ tay để ghi chú
Bước 2: Bạn nên đọc hiểu rõ Phân phối chương trình môn mình muốn cải thiện
Vd: Toán 10 CTST có PPCT như sau:
| BÀI HỌC PHÂN PHỐI CHƯƠNG TRÌNH SGK | Tiết |
| CHƯƠNG I. MỆNH ĐỀ TOÁN HỌC. TẬP HỢP | 7 |
| Bài 1. Mệnh đề toán học | 3 |
| Bài 2. Tập hợp. Các phép toán trên tập hợp | 3 |
| Bài tập cuối chương I | 1 |
| CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN | 6 |
| Bài 1. Bất phương trình bậc nhất hai ẩn | 2 |
| Bài 2. Hệ bất phương trình bậc nhất hai ẩn | 3 |
| Bài tập cuối chương II | 1 |
Bước 3: Bạn tìm hiểu Chương I có bao nhiêu dạng bài tập, mỗi dạng phương pháp giải như thế nào?, những điểm cần lưu ý, lỗi sai thường gặp
Bước 4: Giải bài tập theo từng dạng, giải càng nhiều càng tốt, cứ mỗi bài bạn giải sai bạn sẽ phải xem hướng dẫn giải chi tiết từ đó so sánh chỗ sai của mình xem mình sai ở đâu? tại sao lại sai? trường hợp sai có bao nhiêu trường hợp?
Bước 5: Ghi chú lỗi sai vào sổ tay, nhớ liệt kê lỗi sai theo dạng toán
Bước 6: Cuối kỳ mình chuẩn bị kiểm tra giữa kỳ hoặc cuối kỳ thì lấy sổ tay ra đọc qua 1 lần và tiến hành giải đề, cứ lập lại liên tục trước khi thi sẽ giúp bạn tối đa hoá điểm số trong kỳ thi và đồng thời tránh rất nhiều lỗi sai mà mình đã gặp nếu gặp trong đề thi.
Đó là quá trình mình ôn thi NHƯNG hiện tại có 1 hệ thống giúp bạn quản lý sổ tay như phương pháp ở trên cực kỳ hiệu quả đó là EXAMON
Hệ thống luyện thi Examon được thiết kế giống phương pháp học ở trên tối ưu hoá sổ tay giúp bạn luyện tập hiệu quả hơn gấp 200%
Examon sẽ phân phối chương trình theo từng dạng toán mỗi một dạng toán sẽ có bài tập luyện, quá trình luyện của bạn sẽ được ghi vào sổ tay để AI Examon phân tích đánh giá bạn đang sai ở đâu, lỗi sai thường ở dạng bài tập nào? mức độ bài sai ở Nhận Biết - Thông Hiểu - Vận Dụng - Vận Dụng Cao từ đó Examon sẽ đề xuất các câu tương tự câu sai để bạn luyện tập đi luyện tập lại cứ như thế vòng lặp liên tục giúp học sinh cải thiện kỹ năng giải bài tập đồng thời bao quát tất cả các dạng toán thường sai tránh tối đa những sai sót lúc đi thi.
Ngoài ra hệ thống Examon định hướng học sinh học theo 3 tiêu chí:
1: Rèn luyện khả năng tự học: Tự học luôn là yếu tố quan trọng
2: Học kỹ năng tư duy giải bài: Hầu hết học sinh hiểu bài nhưng không cách nào diễn đạt cho bạn mình hiểu cái mình đang hiểu là do thiếu kỹ năng này
3: Học từ lỗi sai: Nên dành nhiều thời gian để khám phá lỗi sai của chính mình chính là phương pháp học nhanh nhất, học từ cái sai của mình và học từ cái sai của người khác là 1 kỹ năng rất cần thiết cho mọi sự phát triển.
Sơ đồ tối ưu hoá cải thiện Điểm số cho học sinh