Ứng dụng Đạo hàm trong thực tế
Qua bài viết này Examon sẽ cho các bạn thấy rằng Đạo hàm thú vị ra sao. Cùng Examon khám phá ngay nhé!
Mục lục bài viết
Đạo hàm là một kiến thức rất rộng lớn, nó không chỉ giúp ta giải các bài toán trong chương trình phổ thông mà còn ứng dụng để giải quyết các bài liên quan đến đời sống, các lĩnh vực như kinh tế, y học, vật lý, khoa học,...... Để biết giúp bạn biết thêm về các ứng dụng đó, Examon tổng hợp lý thuyết và bài tập ứng dụng một cách rõ ràng và chi tiết nhất. Hãy cùng Examon bước vào thế giới của đạo hàm để khám phá những điều bí ẩn mà có lẽ chưa ai nói cho bạn biết nhé!

1. Định nghĩa và các quy tắc của đạo hàm
1.1 Định nghĩa
ĐỊNH NGHĨA
Cho hàm số \(y=f(x)\) xác định trên khoảng \((a ; b)\) và \(x_{0} \in(a ; b)\).Nếu tồn tại giới hạn (hữu hạn)
\[\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\]thì giới hạn đó được gọi là đạo hàm của hàm số \(y=f(x)\) tại điểm \(x_{0}\) và kí hiệu là \(f^{\prime}\left(x_{0}\right)\) (hoặc \(y^{\prime}\left(x_{0}\right)\) ), tức là
\[f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\]1.2 Quy tắc tính đạo hàm
Giả sử \(u=u(x), v=v(x)\) là các hàm số có đạo hàm tại điểm \(x\) thuộc khoảng xác định.
Ta có:
1. \((k \cdot u)^{\prime}=k \cdot u^{\prime}\) \(k\) là hằng số;
2. \((u+v)^{\prime}=u^{\prime}+v^{\prime}\) Đạo hàm của một tống;
3. \((u \cdot v)^{\prime}=u^{\prime} v+v^{\prime} u\) Đạo hàm của một tích;
4. \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-v^{\prime} u}{v^{2}}, v \neq 0\) Đạo hàm của một thương.
1.3 Ý nghĩa của đạo hàm
Trong hình học, Đạo hàm hỗ trợ về việc tính toán các đường cong và phương trình tiếp tuyến.
Trong lĩnh vực vật lý, đạo hàm được dùng tính toán vận tốc, gia tốc tức thời, cường độ dòng điện tức thời,...... Đạo hàm cho biết tốc độ thay đổi của một hàm số tại mỗi điểm.
Trong kinh tế học, đạo hàm được sử dụng để tối ưu hóa hàm lợi nhuận và tìm ra điểm cực đại hoặc cực tiểu của hàm số. Chúng có thể giúp ta tìm ra giá trị lớn nhất hoặc nhỏ nhất của một hàm số. Từ đó giúp tối ưu hóa các vấn đề thực tế như tối ưu hóa chi phí, tối ưu hóa hiệu suất, v.v.
2. Bảng công thức Đạo hàm đầy đủ
Đạo hàm của hàm sơ cấp Đạo hàm của hàm hợp \(u=u(x)\)
1. \((C)^{\prime}=0, C\) là hằng số
2. \((x)^{\prime}=1\)
3. \(\left(x^{\alpha}\right)^{\prime}=\alpha \cdot x^{\alpha-1}\) \(\left(u^{a}\right)^{\prime}=\alpha \cdot u^{a-1} \cdot u^{\prime}\)
4. \(\left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^{2}}\) \(\left(\frac{1}{u}\right)^{\prime}=-\frac{u^{\prime}}{u^{2}}\)
5. \((\sqrt{x})^{\prime}=\frac{1}{2 \sqrt{x}}\) \((\sqrt{u})^{\prime}=\frac{u^{\prime}}{2 \sqrt{u}}\)
6. \(\left(e^{x}\right)^{\prime}=e^{x}\) \(\left(e^{u}\right)^{\prime}=u^{\prime} \cdot e^{u}\)
7. \(\left(a^{x}\right)^{\prime}=a^{x} \cdot \ln a ; a \in \mathbb{R}^{+} \backslash\{1\}\) \(\left(a^{a}\right)^{\prime}=u^{\prime} \cdot a^{u} \cdot \ln a\)
8. \((\ln x)^{\prime}=\frac{1}{x}\) \((\ln u)^{\prime}=\frac{u^{\prime}}{u}\)
9. \(\left(\log _{a} x\right)^{\prime}=\frac{1}{x \cdot \ln a}\) \(\left(\log _{a} u\right)^{\prime}=\frac{u^{\prime}}{u \cdot \ln a}\)
10. \((\sin x)^{\prime}=\cos x\) \((\sin u)^{\prime}=u^{\prime} \cdot \cos u\)
11. \((\cos x)^{\prime}=-\sin x\) \((\cos u)^{\prime}=-u^{\prime} \cdot \sin u\)
12. \((\tan x)^{\prime}=\frac{1}{\cos ^{2} x}=1+\tan ^{2} x\) \((\tan u)^{\prime}=\frac{u^{\prime}}{\cos ^{2} u}=u^{\prime}\left(1+\tan ^{2} u\right)\)
13. \((\cot x)^{\prime}=\frac{-1}{\sin ^{2} x}=-1\left(1+\cot ^{2} u\right)\) \((\cot u)^{\prime}=\frac{-u^{\prime}}{\sin ^{2} u}=-u^{\prime}\left(1+\cot ^{2} u\right)\)
14. \((\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}\) \((\arcsin u)^{\prime}=\frac{u^{\prime}}{\sqrt{1-u^{2}}}\)
15. \((\arccos x)^{\prime}=\frac{-1}{\sqrt{1-x^{2}}}\) \((\arccos u)^{\prime}=\frac{-u^{\prime}}{\sqrt{1-u^{2}}}\)
16. \((\arctan x)^{\prime}=\frac{1}{1+x^{2}}\) \((\arctan u)^{\prime}=\frac{u^{\prime}}{1+u^{2}}\)
17. \((\operatorname{arccot} x)^{\prime}=\frac{-1}{1+x^{2}}\) \((\operatorname{arccot} u)^{\prime}=\frac{-u^{\prime}}{1+u^{2}}\)
3. Ứng dụng đạo hàm trong thực tế
3.1 Đạo hàm trong Hình học
Bài toán 1. Từ một tấm tôn hình chữ nhật có kích thước là \(a^{\prime} b\) với \(a\lt b\). Người ta cắt bỏ 4 hình vuông bằng nhau ở 4 góc rồi gò thành một hình hộp chữ nhật không có nắp. Hỏi cạnh của hình vuông cắt đi phải bằng bao nhiêu để hình hộp đó có thể tích lớn nhất ?
Phân tích:
- Trước tiên, với câu hỏi của bài toán thì ta nên đặ̆t x chính là cạnh của hình vuông cắt đi. Nhe vậy ta cần tìm điều kiện giới hạn cuia biến số \(\mathrm{x}\). Do khi đó I cạnh của tấm nhôm sau khi bị cắt trở thành \(\mathrm{a}-2 \mathrm{x}\gt 0 \Rightarrow \mathrm{x}\lt \frac{\mathrm{a}}{2}\) nên ta có \(0\lt \mathrm{x}\lt \frac{\mathrm{a}}{2}\).
- Và đồng thời ta cũng có đurơc cạnh cuia tấm nhôm còn lại là \(\mathrm{b}-2 \mathrm{x}\gt 0\). Đến đây ta cần thiết lập công thức tinh thể tich khối hôp \(V=x(a-2 x)(b-2 x)\)
- Bài toán trở thành tìm \(\max _{x \in\left(0 ; \frac{a}{2}\right)} V(x)=?\) Mời bạn đọc xem lời giải.
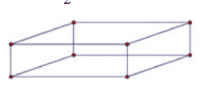
Huớng dẫn giải.
- Gọi \(x\) là cạnh của hình vuông cắt đi, ta phải có điều kiện \(0\lt x\lt \frac{a}{2}\).
Khi đó thể tích hình hộp là \(V=x(a-2 x)(b-2 x)=4 x^{3}-2(a+b) x^{2}+a b x=V(x)\).
- Bài toán trở thành tìm \(\max _{x \in\left(0, \frac{\pi}{2}\right)} V(x)=\) ?
Đạo hàm \(V^{\prime}=f^{\prime}(x)=12 x^{2}-4(a+b) x+a b\).
Ta có \(\Delta^{\prime}=4(a+b)^{2}-12 a b=4\left(a^{2}-a b+b^{2}\right)\gt 0\) với mọi \(a, b\).
Do đó \(V^{\prime}=0\) luôn có hai nghiệm phân biệt
\[\begin{array}{c}x_{1}=\frac{a+b-\sqrt{a^{2}-a b+b^{2}}}{6}\lt x_{2}=\frac{a+b+\sqrt{a^{2}-a b+b^{2}}}{6} \\\text { Theo định lý Vi-et, ta có }\left\{\begin{array}{l}x_{1}+x_{2}=\frac{a+b}{3}\gt 0 \\x_{1} x_{2}=\frac{a b}{12}>0\end{array}\right.\end{array}\]suy ra \(0\lt x_{1}\lt x_{2}\).
Hơn nữa, ta có \(V^{\prime}\left(\frac{a}{2}\right)=f^{\prime}\left(\frac{a}{2}\right)=a^{2}-a b=a(a-b)\lt 0\). Do đó \(0\lt x_{1}\lt \frac{a}{2}\lt x_{2}\).
Bảng biến thiên
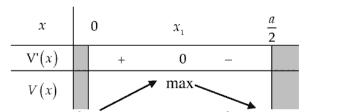
- Dự vào bảng biến thiên ta thấy \(V\) đạt giá trị lớn nhất khi
\[x=x_{1}=\frac{a+b-\sqrt{a^{2}-a b+b^{2}}}{6} \text {. }\]Bài toán 2. Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích \(V\left(\mathrm{~m}^{3}\right)\) không đổi, hệ số \(k\gt 0\) cho trước ( \(k\) là tỉ số giứa chiều cao của hố và chiều rộng của đáy. Hãy xác định các kích thước của đáy để khi xây tiết kiệm nguyên vật liệu nhất?
Phân tích:
- Với thể tich V cho trước và quan hệ giữa chiều rông cuia đáy và chiều cao của hình hộp ta hoàn toàn có thể biểu diễn được độ dài chiều dài theo 1 biến.
- Như vậy ta cần hiểu yêu cầu bài toán "tiết kiệm nguyên vật liệu nhất là gì ?" Đó chính là làm sao cho phần bao phủ bên ngoài hình hộp có diện tich nhỏ nhất hay diện tích toàn phần cuia khối hộp nhỏ nhất.
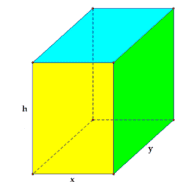
Hướng dẫn giải:
- Gọi \(x, y(0\lt x\lt y)\) lần lượt là chiều rộng và chiều dài của đáy hố ga.
Gọi \(h\) là chiều cao của hố ga \((h\gt 0)\).
- Theo đề bài ta có \(h=k x\) và \(V=h x y \Rightarrow y=\frac{V}{h x}=\frac{V}{k x^{2}}\)
Để tiết kiệm nguyên vật liệu nhất ta cần tìm các kich thước sao cho diện tích toàn phần của hố ga là nhô nhất.
Khi đó ta có: \(S_{t p}=2 x h+2 y h+2 x y=2 x(k x)+2(k x) \cdot \frac{V}{k x^{2}}+2 x \frac{V}{k x^{2}}\)
Suy ra \(S_{t p}=2 k x^{2}+\frac{2\left(\frac{k+1}{k}\right) V}{x}\) Xét hàm số \(f(x)=2 k x^{2}+\frac{2\left(\frac{k+1}{k}\right) V}{x}\).
Bài toán trở thành tìm giá trị nhỏ nhất của \(f(x)\) với \(x\gt 0\).
\[f^{\prime}(x)=4 k x-\frac{2\left(\frac{k+1}{k}\right) V}{x^{2}}=2 \frac{2 k^{2} x^{3}-(k+1) V}{k x^{2}}, \text { cho } f^{\prime}(x)=0 \Leftrightarrow x_{o}=\sqrt[3]{\frac{(k+1) V}{2 k^{2}}}>0\]Lập bảng biến thiên ta có
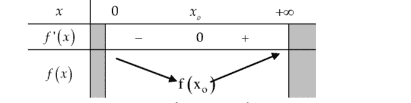
Dựa vào bảng biến thiên ta có \(\min _{x>0} f(x)=f\left(\sqrt[3]{\frac{(k+1) V}{2 k^{2}}}\right)\).
Khi đó \(y=\sqrt[3]{\frac{4 k V}{(k+1)^{2}}}\) và \(h=\sqrt[3]{\frac{k(k+1) V}{2}}\).
3.2 Đạo hàm trong Vật lý
Bài toán 1. Một chất điểm chuyển động theo quy luật \(s(t)=6 t^{2}-t^{3}-9 t+1, \mathrm{~s}\) tính theo mét, \(\mathrm{t}\) tính theo giây. Trong 5 giây đầu tiên, thời điểm \(\mathrm{t}\) mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất là:
A. \(t=3\).
B. \(t=1\).
C. \(t=2\).
D. \(t=4\).
Phân tích:
- Với kiến thức Vật lý đã học, ta biết \(\mathrm{v}(\mathrm{t})=\mathrm{s}^{\prime}(\mathrm{t})\). Do đó để tìm giá trị lớn nhất trong 5 giây đầu tiên \(\mathrm{t} \in[0 ; 5]\) thi ta chi cần vận dụng kiến thức đạo hàm đã học.
Huớng dẫn giäi
\[v(t)=s^{\prime}(t)=12 t-3 t^{2}-9, v^{\prime}(t)=-6 t+12, v^{\prime}(t)=0 \Leftrightarrow t=2 \text {. }\]Lập bảng biến thiên ta có:
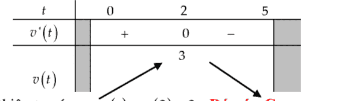
Dựa vào bảng biến thiên ta có \(\max _{\mathrm{t} \in(0 ; 5)} \mathrm{v}(\mathrm{t})=\mathrm{v}(2)=3\).. Đáp án \(C\).
Bài toán 2. Một nguồn điện với suất điện động \(E\) và điện trở \(r\) được nối với một biến trờ \(R\) như hình vẽ. Với giá trị nào của biến trờ thì công suất tỏa nhiệt trên toàn mạch sẽ đạt cực đại ?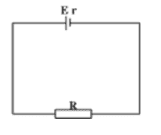
A. \(r=R\).
B. \(r=2 R\).
C. \(r=3 R\).
D. \(r=4 R\).
Phân tích:
- Để làm đượđược dang toán này, trước tiên ta cần có kiến thúc về dòng điện 1 chiều đãa học ờ lớp duoơit: công suất tòa nhiệt trên toàn mạch sẽ là \(P=R I^{2}\) và đồng thời cuờng âộ dòng điện trong mach sẽ là \(I=\frac{E}{R+r}\).
- Đến đây ta thấy \(P\) có thể tính theo \(R\) và r. Và do đó ta có thể vận dụng kiến thúc về đạo hàm để tìm giá trị lớn nhất, nhỏ nhất cùa biểu thúc P.
Hướng dẫn giải:
Theo công thức công suất tỏa nhiệt ta có \(P=R I^{2}\) với \(I=\frac{E}{R+r}\)
\(\Rightarrow P=\frac{R E^{2}}{(R+r)^{2}}(R\gt 0)\). Xét hàm số \(f(R)=\frac{R E^{2}}{(R+r)^{2}}\) với \(R>0\)
Ta tìm \(f^{\prime}(R)=E^{2} \frac{(R+r)^{2}-2 R(R+r)}{(R+r)^{4}}=E^{2} \frac{r-R}{(R+r)^{3}}, f^{\prime}(R)=0 \Leftrightarrow r=R\)
Lập bảng biến thiên ta có:
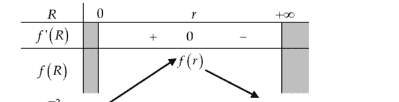
suy ra \(\max f(R)=f(r)=\frac{E^{2}}{4 r}\). Ta chọn đáp án A.
3.3 Đạo hàm trong Kinh tế
Bài toán 1. Một công ty đánh giá rằng sẽ bán được \(N\) lô hàng nếu tiêu phí hết số tiền là \(x\) (triệu đồng) vào việc quảng cáo. Biết rằng \(N\) và \(x\) liên hệ với nhau bằng biểu thức \(N(x)=-x^{2}+30 x+6,0 \leq x \leq 30\). Hãy tìm số lô hàng lớn nhất mà công ty có thể bán sau đợt quảng cáo và số tiền đã dành cho việc quảng cao đó ?
Huớng dẫn giải.
Ta có: \(N(x)=-x^{2}+30 x+6 \Rightarrow N^{\prime}(x)=-2 x+30 \Rightarrow N^{\prime}(x)=0 \Leftrightarrow x=15\)Đồng thời \(\left\{\begin{array}{l}N(0)=6 \\ N(15)=231 \\ N(30)=6\end{array} \Rightarrow \max _{x \in[0 ; 30]} N(x)=231 \Leftrightarrow x=15\right.\).
Vậy, nếu công ty dành 15 triệu cho việc quảng cáo thì công ty sẽ bán được nhiều nhất là 231 lô hàng.
Bài toán 2: Một công ty nhận sản xuất 400.000 huy chương bạc nhân ngày kỷ niệm lần thứ 30 Apollo 11 đổ bô lên mặt Trăng. Công ty sở hữu 20 máy, mỗi máy có thể sản xuất 200 huy chương/giờ.
Chi phí lắp đặt máy để sản xuất huy chương là 80 USD/máy và tổng chi phí vận hành là 5,76 USD/giờ. Hãy biểu diễn chi phí sản xuât 400.000 huy chương bằng một hàm theo số máy đã dùng. Hãy uớc tính số máy mà công ty nên dùng đề chi phí nhỏ nhất.
Hướng dẫn giải
Gọi \(x(1 \leq x \leq 20, x \in \square)\) là số máy sử dụng và \(C(x)\) là hàm tổng chi phí sản xuất tương ứng.
Chi phí lắp đặt các máy là \(80 x\)
Chi phí vận hành các máy là \(\frac{400000}{200 x} \cdot 5,76\)
Tổng chi phí \(=\) Chi phí lắp đặt + Chi phí vận hành \(\Rightarrow C(x)=80 x+\frac{11520}{x}\)
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số \(C(x)\) với \(x \in[1 ; 20]\)
Ta có \(C^{\prime}(x)=80-\frac{11520}{x^{2}} \Rightarrow C^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=12(\mathrm{tm}) \\ x=-12(\mathrm{ktm})\end{array}\right.\)
Đồng thời \(\left\{\begin{array}{l}C(1)=11600 \\ C(20)=2176 \\ C(12)=1920\end{array} \Rightarrow \max _{x \in[1: 20]} C(x)=C(12)=1920 \Leftrightarrow x=12\right.\)
Vậy công ty nên sử dụng 12 máy để sản xuất thì tổng chi phí sẽ nhỏ nhất.
3.4 Đạo hàm trong đời sống và lĩnh vực khác
Bài toán 1: (Ứng dụng trong Sinh học). Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định được số lượng vi khuẩn tăng theo thời gian bởi qui luật \(N(t)=1000+\frac{100 t}{100+t^{2}}\) (con vi khuẩn), trong đó \(t\) là thời gian (đơn vị giây)). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào, số lượng vi khuẩn tăng lên là lớn nhất ?
Phân tích:
- Tương tự như những bài toán truớc, do đề bài đã mô hình hóa bài toán durới dạng hàm nên ta chi cần vận dụng kiến thức đạo hàm là có thể tìm được số lượng tăng nhanh nhất cuia vi khuẩn.
Huớng dẫn giải
Ta có tốc độ phát triển của đàn vi khuẩn tại thời điểm \(t\) là
\[N^{\prime}(t)=\frac{100\left(100+t^{2}\right)-100 t(2 t)}{\left(100+t^{2}\right)^{2}}=\frac{100^{2}-100 t^{2}}{\left(100+t^{2}\right)^{2}}(\forall t\gt 0)\]Xét \(N^{\prime}(t)=0 \Leftrightarrow t^{2}=100 \Leftrightarrow t=10>0\).
Lâp bảng biến thiên ta được:
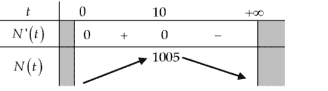
Dựa vào bảng biến thiên, ta kết luận \(\max N(t)=N(10)=1005\).
Bài toán 2: (Ứng dụng trong Y Học). Độ giảm huyết áp của bệnh nhân được cho bời công thức \(G(x)=0,025 x^{2}(30-x)\) với \(x\) là liều lượng thuốc được tiêm cho bệnh nhân ( \(x:\) miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm?
Phân tích:
- Tương tự như những bài toán đã cho sã̃n hàm số, thì việc ứng dụng đạo hàm không còn quá khó khăn nữa.
Huớng dẫn giải.
\[G(x)=\frac{1}{40} x^{2}(30-x)=\frac{1}{40}\left(30 x^{2}-x^{3}\right) \Rightarrow G^{\prime}(x)=\frac{1}{40}\left(60 x-3 x^{2}\right)\]Cho \(G^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=20 \\ x=0(k t m)\end{array}\right.\)
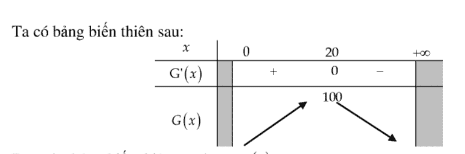
Dựa vào bảng biến thiên ta có \(\max G(x)=100 \Leftrightarrow x=20\).
4. Học đạo hàm như thế nào?
Để ghi nhớ hết tất cả các công thức cũng như lý thuyết đạo hàm là một điều rất khó khăn. Vì Đạo hàm có quá nhiều thứ phải học, phải ghi nhớ dẫn đến việc bạn không thể đạt điểm cao trong các kỳ thi. Do đó Examon đã ở đây để giúp bạn. Examon nghiên cứu ra một phương pháp học giúp bạn cải thiện điểm số trong các kỳ thi và cũng sẽ giúp bạn học đạo hàm một cách dễ dàng hơn.
PHƯƠNG PHÁP HỌC HIỆU QUẢ [ĐẠO HÀM]
Có bao giờ bạn tự hỏi tại sao điểm kiểm tra của mình thấp không?
Mình cũng từng bị như vậy và luôn hỏi tại sao suốt 1 thời gian dài và giờ mình đã tìm ra câu trả lời “Đó chính là phương pháp học không đúng".
Để học hiệu quả bạn nên làm những gì?
Đầu tiên nên thiết kế lộ trình bứt phá điểm số của mình như sau:
Bước 1: Bạn cần có 1 cuốn sổ tay để ghi chú
Bước 2: Bạn nên đọc hiểu rõ Phân phối chương trình môn mình muốn cải thiện
Vd: Toán 10 CTST có PPCT như sau:
| BÀI HỌC PHÂN PHỐI CHƯƠNG TRÌNH SGK | Tiết |
| CHƯƠNG I. MỆNH ĐỀ TOÁN HỌC. TẬP HỢP | 7 |
| Bài 1. Mệnh đề toán học | 3 |
| Bài 2. Tập hợp. Các phép toán trên tập hợp | 3 |
| Bài tập cuối chương I | 1 |
| CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN | 6 |
| Bài 1. Bất phương trình bậc nhất hai ẩn | 2 |
| Bài 2. Hệ bất phương trình bậc nhất hai ẩn | 3 |
| Bài tập cuối chương II | 1 |
Bước 3: Bạn tìm hiểu Chương I có bao nhiêu dạng bài tập, mỗi dạng phương pháp giải như thế nào?, những điểm cần lưu ý, lỗi sai thường gặp
Bước 4: Giải bài tập theo từng dạng, giải càng nhiều càng tốt, cứ mỗi bài bạn giải sai bạn sẽ phải xem hướng dẫn giải chi tiết từ đó so sánh chỗ sai của mình xem mình sai ở đâu? tại sao lại sai? trường hợp sai có bao nhiêu trường hợp?
Bước 5: Ghi chú lỗi sai vào sổ tay, nhớ liệt kê lỗi sai theo dạng toán
Bước 6: Cuối kỳ mình chuẩn bị kiểm tra giữa kỳ hoặc cuối kỳ thì lấy sổ tay ra đọc qua 1 lần và tiến hành giải đề, cứ lập lại liên tục trước khi thi sẽ giúp bạn tối đa hoá điểm số trong kỳ thi và đồng thời tránh rất nhiều lỗi sai mà mình đã gặp nếu gặp trong đề thi.
Đó là quá trình mình ôn thi NHƯNG hiện tại có 1 hệ thống giúp bạn quản lý sổ tay như phương pháp ở trên cực kỳ hiệu quả đó là EXAMON
Hệ thống luyện thi Examon được thiết kế giống phương pháp học ở trên tối ưu hoá sổ tay giúp bạn luyện tập hiệu quả hơn gấp 300%
Examon sẽ phân môn theo chương theo dạng toán mỗi một dạng toán sẽ có bài tập luyện, quá trình luyện của bạn sẽ được ghi vào sổ tay để AI Examon phân tích đánh giá bạn đang sai ở đâu, lỗi sai thường ở dạng bài tập nào? mức độ bài sai ở Nhận Biết - Thông Hiểu - Vận Dụng - Vận Dụng Cao từ đó Examon sẽ đề xuất các câu tương tự câu sai để bạn luyện tập đi luyện tập lại cứ như thế vòng lặp liên tục giúp học sinh cải thiện kỹ năng giải bài tập đồng thời bao quát tất cả các dạng toán thường sai tránh tối đa những sai sót lúc đi thi.
Ngoài ra hệ thống Examon định hướng học sinh học theo 3 tiêu chí:
1: Rèn luyện khả năng tự học: Tự học luôn là yếu tố quan trọng
2: Học kỹ năng tư duy giải bài: Hầu hết học sinh hiểu bài nhưng không cách nào diễn đạt cho bạn mình hiểu cái mình đang hiểu là do thiếu kỹ năng này
3: Học từ lỗi sai: Nên dành nhiều thời gian để khám phá lỗi sai của chính mình chính là phương pháp học nhanh nhất, học từ cái sai của mình và học từ cái sai của người khác là 1 kỹ năng rất cần thiết cho mọi sự phát triển.