Bài tập Tính thể tích vật thể quay
Để tính thể tích của một vật thể khi nó được tạo thành bằng cách quay một vùng phẳng quanh một trục cố định, chúng ta thường sử dụng các phương pháp tích phân.
Mục lục bài viết
Một trong những ứng dụng quan trọng của nguyên hàm là tính thể tích của một vật thể khi nó quay quanh một trục. Có hai phương pháp chính để tính thể tích cảu vật thể quay: phương pháp đĩa và phương pháp vỏ trụ. Sau đây chúng ta sẽ cùng thảo luận về 2 phương pháp này.

1. Phương pháp đĩa
Phương pháp này thường được sử dụng khi vật thể quay quanh trục hoành / tung. Thể tích V của vật thể quay được tính bằng tích phân của diện tích mặt cắt đĩa vuông góc với trục quay.
Công thức khi quay quanh trục hoành:
\[V=\pi \int_{a}^{b}[f(x)]^{2} d x\]VD: Tính thể tích vật thể tạo thành khi quay vùng phẳng giới hạn bởi \(y=\sqrt{x}, x=0\) và \(x=4\) quanh trục hoành.
Bước 1: Xác định hàm số và giới hạn
\[f(x)=\sqrt{x}, \quad a=0, \quad b=4\]Bước 2: Lập biểu thức tích phân
\[V=\pi \int_{0}^{4}(\sqrt{x})^{2} d x=\pi \int_{0}^{4} x d x\]Bước 3: Tính nguyên hàm
\[\pi \int_{0}^{4} x d x=\pi\left[\frac{x^{2}}{2}\right]_{0}^{4}=\downarrow\left(\frac{4^{2}}{2}-\frac{0^{2}}{2}\right)=\pi\left(\frac{16}{2}\right)=8 \pi\]=> V=\(8 \pi\)
2. Phương pháp vỏ trụ
Phương pháp này thường được sử dụng khi vật thể quay quanh trục không phải là trục hoành / tung. Thể tích V của vật thể quay được tính bằng tích phân của diện tích mặt cắt vỏ trụ.
Công thức khi quay quanh trục tung:
\[V=2 \pi \int_{a}^{b} x f(x) d x\]VD: Tính thể tích vật thể tạo thành khi quay vùng phẳng giới hạn bởi \(y=x^{2}, x=0\) và \(x=\) 1 quanh truc tung.
Bước 1: Xác định hàm số và giới hạn
\[f(x)=x^{2}, \quad a=0, \quad b=1\]Bước 2: Lập biểu thức tích phân
\[V=2 \pi \int_{0}^{1} x\left(x^{2}\right) d x=2 \pi \int_{0}^{1} x^{3} d x\]Bước 3: Tính nguyên hàm
\[2 \pi \int_{0}^{1} x^{3} d x=2 \pi\left[\frac{x^{4}}{4}\right]_{0}^{1}=2 \pi\left(\frac{1^{4}}{4}-\frac{0^{4}}{4}\right)=2 \pi\left(\frac{1}{4}\right)=\frac{\pi}{2}\]=> V=\(\frac{\pi}{2}\)
3. Bài tập tăng cường
3.1. Bài tập 1
Một vật thể tròn xoay sinh ra bởi phép quay xung quanh trục \(O x\) của hình giới hạn bời trục \(O x\) và đường \(y=\sin x,(0 \leq x \leq \pi)\) như hình vẽ
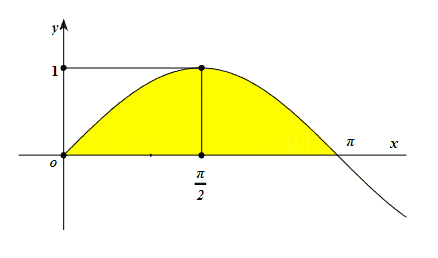
Tính thể tích vật thể:
giải:
Ta có:
\(V=\pi \int_{0}^{\pi} \sin ^{2} x d x=\pi \int_{0}^{\pi} \frac{1-\cos 2 x}{2} d x\)
\(=\left.\frac{\pi}{2}\left(x-\frac{\sin 2 x}{2}\right)\right|_{0} ^{\pi}=\frac{\pi^{2}}{2}\)
3.2. Bài tập 2
Gọi \(V\) là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=0\) và \(x=4\) quanh trục \(O x\). Đường thẳng \(x=a(0\lt a\lt 4)\) cắt đồ thị hàm \(y=\sqrt{x}\) tại \(M\) (hình vẽ sau).
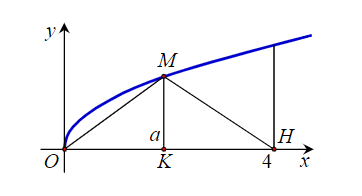
Gọi \(V_{1}\) là thể tích khối tròn xoay tạo thành khi quay tam giác \(O M H\) quanh trục \(O x\). Biết rằng \(V=2 V_{1}\). Tính a
giải:
Ta có \(\sqrt{x}=0 \Leftrightarrow x=0\). Khi đó \(V=\pi \int_{0}^{4} x \mathrm{~d} x=8 \pi\)
Ta có \(M(a ; \sqrt{a})\)Khi quay tam giác \(O M H\) quanh trục \(O x\) tạo thành hai hình nón có chung đáy:
- Hình nón \(\left(N_{1}\right)\) có đĩnh là \(O\), chiều cao \(h_{1}=O K=a\), bán kính đáy \(R=M K=\sqrt{a}\);
- Hình nón \(\left(N_{2}\right)\) thứ 2 có đỉnh là \(H\), chiều cao \(h_{2}=H K=4-a\), bán kính đáy \(R=M K=\sqrt{a}\)
Khi đó \(V_{1}=\frac{1}{3} \pi R^{2} h_{1}+\frac{1}{3} \pi R^{2} h_{2}\)
\(=\frac{1}{3} \pi(\sqrt{a})^{2} \cdot a+\frac{1}{3} \pi(\sqrt{a})^{2} \cdot(4-a)=\frac{4}{3} \pi a\)
Theo đề bài \(V=2 V_{1} \Leftrightarrow 8 \pi=2 \cdot \frac{4}{3} \pi a \Rightarrow a=3\).
Kết lại các phương pháp
Hai phương pháp chính để tính thể tích của vật thể quay là phương pháp đĩa và phương pháp võ trụ. Việc chọn phương pháp nào phụ thuộc vào trụ quay và dạng của vùng phẳng.
Cả hai phương pháp đều dựa trên tích phân và sử dụng nguyên hàm để tính toán diện tích và thể tích. Việc hiểu rõ và áp dụng đúng các bước sẽ giúp chúng ta giải quyết nhiều bài toán về thể tích trong thực tế.
Từ tiêu chí số \(\mathbf{3} \mathbf{H o ̣c}\) từ lỗi sai đội ngũ chuyên môn đã nghiên cứu cách học và phát triển thành công công nghệ Al Gia sư Toán Examon với tính năng vượt trội hỗ trợ người học trong quá trình làm bài tập trên hệ thống đề thi Examon.
Thầy/cô Al sẽ ghi lại tất cả các lỗi sai của bạn đưa về hệ thống trung tâm dữ liệu để phân tích nhằm phát hiện năng lực của từng học sinh từ đó đưa ra các đề xuất bài tập phù hợp với từng bạn
Nhằm giúp người học rút ngắn thời gian luyện tập những kiến thức bị hỏng hoặc yếu nhất của mình tiến đến cải thiện kỹ năng làm bài thi giúp nhanh cán mốc ĐIẾM SỐ mình hằng mong ước
Bộ đề cho mọi kì thi
Với các lớp học truyền thống chỉ sử dụng một bộ giáo trình duy nhất thực sự là một thách thức cho giáo viên, vì mỗi học sinh đều có năng lực riêng biệt.
Có học sinh giỏi phần tích phân nhưng yếu phần xác suất, việc học thêm như vậy sẽ khiến các em mất gấp đôi thời gian, điều này không cần thiết.
Thay vào đó, nếu học sinh có thể tiết kiệm một nửa thời gian để luyện thêm phần vectơ, thì sẽ rút ngắn được thời gian luyện tập và tăng hiệu quả học tập.
Với những băn khoăn này, đội ngũ sáng lập Examon đã phát triển một sản phẩm hỗ trợ học tập hiệu quả và cá nhân hóa việc học theo từng năng lực của học sinh.
Với sự hỗ trợ của Gia sư Al, học sinh sẽ có trải nghiệm học tập tức thì và cải thiện điểm số nhanh chóng, lên đến \(200 \%\).
Hệ thống Examon thiết kế hỗ trợ người học với 3 tiêu chí sau:
Thứ 1: Rèn luyện khả năng tự học: Tự học luôn là yếu tố quan trọng quyết định
Thứ 2: Học kỹ năng tư duy giải bài: Hầu hết học sinh hiểu bài nhưng không cách nào diễn đạt cho bạn mình hiểu cái mình đang hiểu là do thiếu kỹ năng này
Thứ 3: Học từ lỗi sai: Nên dành nhiều thời gian để khám phá lỗi sai của chính mình chính là phương pháp học nhanh nhất, học từ cái sai của mình và học từ cái sai của người khác là 1 kỹ năng rất cần thiết cho mọi sự phát triển.
