Tổng hợp lý thuyết và bài tập ĐẠO HÀM
Để Examon tổng hợp lý thuyết và bài tập ĐẠO HÀM giúp bạn nhé!
Mục lục bài viết
Đạo hàm không chỉ là một công cụ toán học khô khan mà nó còn là một kiến thức thú vị bởi nó là giúp chúng ta hiểu hơn về tốc độ thay đổi và động lực của mọi thứ, từ quỹ đạo của các hành tinh đến sự biến đổi trong thị trường tài chính.
Ứng dụng đạo hàm vào thực tiễn có gì thú vị? Nó có liên quan gì đến kinh tế, thị trương tài chính, nghiên cứu khoa học? Để giải đáp hết những thắc mắc trên Examon đã tổng hợp những kiến thức quan trọng và một số ứng dụng của nó một cách cô động nhất để giúp bạn hiểu thêm về sự bí ẩn mà chưa ai giải đáp cho bạn và đập tan nỗi sợ đạo hàm của bạn.

1. Giới thiệu ĐẠO HÀM
1.1 Định nghĩa
ĐỊNH NGHĨA
Cho hàm số \(y=f(x)\) xác định trên khoảng \((a ; b)\) và \(x_{0} \in(a ; b)\).Nếu tồn tại giới hạn (hữu hạn)
\[\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\]thì giới hạn đó được gọi là đạo hàm của hàm số \(y=f(x)\) tại điểm \(x_{0}\) và kí hiệu là \(f^{\prime}\left(x_{0}\right)\) (hoặc \(y^{\prime}\left(x_{0}\right)\) ), tức là
\[f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\]!!!CHÚ Ý
Đại lượng \(\Delta x=x-x_{0}\) : gọi là số gia của biến số tại \(x_{0}\).
Đại lượng \(\Delta y=f(x)-f\left(x_{0}\right)=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)\) : gọi là số gia của hàm số.
1.2 Quy tắc
- Các quy tắc cơ bản trong đạo hàm
Giả sử \(u=u(x), v=v(x)\) là các hàm số có đạo hàm tại điểm \(x\) thuộc khoảng xác định.
Ta có:
1. \((k \cdot u)^{\prime}=k \cdot u^{\prime}\) \(k\) là hằng số;
2. \((u+v)^{\prime}=u^{\prime}+v^{\prime}\) Đạo hàm của một tống;
3. \((u \cdot v)^{\prime}=u^{\prime} v+v^{\prime} u\) Đạo hàm của một tích;
4. \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-v^{\prime} u}{v^{2}}, v \neq 0\) Đạo hàm của một thương.
1.3 Đạo hàm cấp cao
ĐỊNH NGHĨA
Giả sử hàm số \(y=f(x)\) có đạo hàm \(f^{\prime}(x)\)
- Đạo hàm của hàm số f'(x), nếu có, được gọi là đạo hàm cấp hai của hàm số f(x), kí hiệu là y" hay f"(x).
- Đạo hàm của hàm số f" (x), nếu có, được gọi là đạo hàm câp ba của hàm số \(f(x)\), kí hiệu là y" hay f"'(x).
- Tương tự, đạo hàm của đạo hàm cấp ( \(n-1)\) được gọi là đạo hàm cấp \(n\) của hàm số \(y=f(x)\), kí hiệu là \(y^{(n)}\) hay \(f^{(n)}(x)\)
\(f^{(n)}(x)=\left[f^{(n-1)}(x)\right]^{\prime}\), với \(\mathrm{n}\) thuộc \(\mathrm{Z}\) và \(\mathrm{n}\gt =2\)
CÔNG THỨC ĐẠO HÀM CẤP CAO
\(\begin{array}{l}\left(x^{m}\right)^{(n)}=m(m-1) \ldots(m-n+1) \cdot x^{m-n} . \\ (\ln x)^{(n)}=\frac{(-1)^{n-1}(n-1)!}{x^{n}} . \\ \left(a^{x}\right)^{(n)}=a^{x} \cdot \ln ^{n} a, \text { với a }\gt 0 . \\ (\sin x)^{(n)}=\sin \left(x+n \frac{\pi}{2}\right) . \\ (\cos x)^{(n)}=\cos \left(x+n \frac{\pi}{2}\right) \\ \left(e^{x}\right)^{(n)}=e^{x} . \\ \left(\frac{1}{x}\right)^{(n)}=(-1)^{n} \cdot n!. x^{-n-1} .\end{array}\)
Công thức Lepnit
Nếu u và v là các hàm khả vi \(\mathrm{n}\) lần thì: \((u v)^{(n)}=\sum_{k=0}^{n} C_{n}^{k} u^{(k)} \cdot v^{(n-k)}\).
với \(C_{n}^{k}\) kí hiệu tổ hợp chập k của n phần tử:
\[C_{n}^{k}=\frac{n(n-1) \ldots(n-k+1)}{k!}\]1.4 Ứng dụng của đạo hàm
- Tìm cực trị của hàm số: Đạo hàm được sử dụng để tìm các điểm cực đại, cực tiểu của hàm số băng cách giải phương trình \(f^{'}{\left( x \right )} = 0\).
- Khảo sát sự biến thiên của hàm số: Dựa vào dấu của đạo hàm \(f^{'}{\left( x \right )}\), ta xác định khoảng tăng, giảm của hàm số.
- Giá trị lớn nhất, giá trị nhỏ nhất: đạo hàm được sử dụng để xác định giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng xác định. Quy trình thường gồm: Tính đạo hàm của hàm số 𝑓′(𝑥). Tìm nghiệm của phương trình 𝑓′(𝑥)=0 để xác định các điểm tới hạn. Đánh giá hàm số tại các điểm tới hạn và các điểm biên của khoảng để xác định giá trị lớn nhất và nhỏ nhất.
- Tính toán các bài toán thực tế: Đạo hàm được áp dụng trong các bài toán tôí ưu hóa và các bài toán liên quan đến tốc độ và gia tốc.
2. Bảng công thức đạo hàm đầy đủ
Đạo hàm của hàm sơ cấp Đạo hàm của hàm hợp \(u=u(x)\)
1. \((C)^{\prime}=0, C\) là hằng số
2. \((x)^{\prime}=1\)
3. \(\left(x^{\alpha}\right)^{\prime}=\alpha \cdot x^{\alpha-1}\) \(\left(u^{a}\right)^{\prime}=\alpha \cdot u^{a-1} \cdot u^{\prime}\)
4. \(\left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^{2}}\) \(\left(\frac{1}{u}\right)^{\prime}=-\frac{u^{\prime}}{u^{2}}\)
5. \((\sqrt{x})^{\prime}=\frac{1}{2 \sqrt{x}}\) \((\sqrt{u})^{\prime}=\frac{u^{\prime}}{2 \sqrt{u}}\)
6. \(\left(e^{x}\right)^{\prime}=e^{x}\) \(\left(e^{u}\right)^{\prime}=u^{\prime} \cdot e^{u}\)
7. \(\left(a^{x}\right)^{\prime}=a^{x} \cdot \ln a ; a \in \mathbb{R}^{+} \backslash\{1\}\) \(\left(a^{a}\right)^{\prime}=u^{\prime} \cdot a^{u} \cdot \ln a\)
8. \((\ln x)^{\prime}=\frac{1}{x}\) \((\ln u)^{\prime}=\frac{u^{\prime}}{u}\)
9. \(\left(\log _{a} x\right)^{\prime}=\frac{1}{x \cdot \ln a}\) \(\left(\log _{a} u\right)^{\prime}=\frac{u^{\prime}}{u \cdot \ln a}\)
10. \((\sin x)^{\prime}=\cos x\) \((\sin u)^{\prime}=u^{\prime} \cdot \cos u\)
11. \((\cos x)^{\prime}=-\sin x\) \((\cos u)^{\prime}=-u^{\prime} \cdot \sin u\)
12. \((\tan x)^{\prime}=\frac{1}{\cos ^{2} x}=1+\tan ^{2} x\) \((\tan u)^{\prime}=\frac{u^{\prime}}{\cos ^{2} u}=u^{\prime}\left(1+\tan ^{2} u\right)\)
13. \((\cot x)^{\prime}=\frac{-1}{\sin ^{2} x}=-1\left(1+\cot ^{2} u\right)\) \((\cot u)^{\prime}=\frac{-u^{\prime}}{\sin ^{2} u}=-u^{\prime}\left(1+\cot ^{2} u\right)\)
14. \((\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}\) \((\arcsin u)^{\prime}=\frac{u^{\prime}}{\sqrt{1-u^{2}}}\)
15. \((\arccos x)^{\prime}=\frac{-1}{\sqrt{1-x^{2}}}\) \((\arccos u)^{\prime}=\frac{-u^{\prime}}{\sqrt{1-u^{2}}}\)
16. \((\arctan x)^{\prime}=\frac{1}{1+x^{2}}\) \((\arctan u)^{\prime}=\frac{u^{\prime}}{1+u^{2}}\)
17. \((\operatorname{arccot} x)^{\prime}=\frac{-1}{1+x^{2}}\) \((\operatorname{arccot} u)^{\prime}=\frac{-u^{\prime}}{1+u^{2}}\)
3. Bài tập cơ bản
3.1 Bài toán tính đạo hàm bằng định nghĩa
PHƯƠG PHÁP:
- Cần nhớ công thức: \(f^{\prime}(x)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\)
- Phương pháp tính giới hạn của hàm số
VÍ DỤ MINH HỌA:
Ví dụ 1. Cho hàm số \(f(x)=2 x^{2}+x+1\). Tính \(f^{\prime}(2)\) ?
Lời giải
Ta có \(f^{\prime}(2)=\lim _{x \rightarrow 2} \frac{f(x)-f(2)}{x-2}=\lim _{x \rightarrow 2} \frac{2 x^{2}+x+1-11}{x-2}=\lim _{x \rightarrow 2} \frac{(x-2)(2 x+5)}{x-2}=\lim _{x \rightarrow 2}(2 x+5)=9\)
Ví dụ 2. Cho hàm số \(y=x^{3}-2 x+1\). Tính \(y^{\prime}(2)\) ?
Lời giải
Ta có \(y^{\prime}(2)=\lim _{x \rightarrow 1} \frac{y(x)-y(1)}{x-1}=\lim _{x \rightarrow 1} \frac{x^{3}-2 x+1-0}{x-1}\)\(=\lim _{x \rightarrow 1} \frac{(x-1)\left(x^{2}+x-1\right)}{x-1}=\lim _{x \rightarrow 1}\left(x^{2}+x-1\right)=1\).
3.2 Bài toán tính bằng các quy tắc đạo hàm
Quy tắc tính đạo hàm
(1) \((u+v-w)^{\prime}=u^{\prime}+v^{\prime}-w^{\prime}\)
(2)\((u . v)^{\prime}=u^{\prime} v+v^{\prime} u\)
(3) \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-v^{\prime} u}{v^{2}}\)
(4) \((k u)^{\prime}=k \cdot u^{\prime}(k \in \mathbb{R})\)
Đạo hàm sơ cấp:
\(\begin{array}{l}+(C)^{\prime}=0(C \in \mathbb{R}) \\ +\left(x^{*}\right)^{\prime}=n \cdot x^{n-1} \quad\left(n \in \mathbb{N}^{*}\right)\end{array}\)
\(\begin{array}{l}+(\sqrt{x})^{\prime}=\frac{1}{2 \sqrt{x}}(x\gt 0) \\ +\left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^{2}}(x \neq 0)\end{array}\)
Đạo hàm hàm hợp:
\(\cdot\) \(\left(u^{e}\right)^{\prime} n \cdot u^{n-1} \cdot u^{\prime}\left(n \in \mathbb{N}^{+}\right)\)
\(\begin{array}{l}(\sqrt{u})^{\prime}=\frac{u^{\prime}}{2 \sqrt{u}}(u\gt 0) \\ \left(\frac{1}{u}\right)^{\prime}=-\frac{u^{\prime}}{u^{2}}(u \neq 0)\end{array}\)
Các công thức tính nhanh:
\(\begin{array}{l}+\left(\frac{a x+b}{c x+d}\right)^{\prime}=\frac{a d-b c}{(c x+d)^{2}} \\ +\left(\frac{a x^{2}+b x+c}{d x+e}\right)^{\prime}=\frac{a d x^{2}+2 a e x+(b e-c d)}{(d x+e)^{2}} \\ +\left(\frac{a_{1} x^{2}+b_{1} x+c_{1}}{a_{2} x^{2}+b_{2} x+c_{2}}\right)^{\prime}=\frac{\left|\begin{array}{cc}a_{1} & b_{1} \\ a_{2} & b_{2}\end{array}\right| x^{2}+2\left|\begin{array}{ll}a_{1} & c_{1} \\ a_{2} & c_{2}\end{array}\right| x+\left|\begin{array}{ll}b_{1} & c_{1} \\ b_{2} & c_{2}\end{array}\right|}{\left(a_{2} x^{2}+b_{2} x+c_{2}\right)^{2}}\end{array}\)
3.3 Dạng toán chứng minh, giải phương trình, bất phương trình
PHƯƠNG PHÁP:
- Tính \(y^{\prime}\).
\(-\) Dùng các kiến thức đã học để rút gọn, biến đồi về phương trinh hoặc bất phương trình đã biết cách giaii như phương trình bậc nhất, bậc hai, bậc ba (sử dụng máy tính cầm tay).
- Đối vơi bải toán chưmg minh bất đẵng thức thi ta biến đồi vế phức tạp thành vế đơn giản hoặc biến đồi cả hai vế cùng bằng một biểu thức trung gian.
Một số bài toán tìm nghiệm của phương trình bậc hai thỏa mãn điều kiện cho trước.
Cho phưong trình \(a x^{2}+b x+c=0\left({ }^{*}\right)\) vói \(a \neq 0\).
1. Nếu phurơng trình (*) có hai nghiệm \(x_{1}, x_{2}\) thi \(\left\{\begin{array}{l}S=x_{1}+x_{2}=-\frac{b}{a} \\ P=x_{1} x_{2}=\frac{c}{a}\end{array}\right.\).
2. Phương trình \(\left.{ }^{*}{ }^{*}\right)\) có hai nghiệm trái dấu khi và chi khi \(a c\lt 0\).
3. Phương trinh (*) có hai nghiệm durơng phân biệt khi và chi khi \(\left\{\begin{array}{l}\Delta\gt 0 \\ S=-\frac{b}{a}>0 \text {. } \\ P=\frac{c}{a}>0\end{array}\right.\)
4. Phưong trình \(\left.{ }^{*}\right)\) có hai nghiệm âm phân biệt khi và chi khi \(\left\{\begin{array}{l}\Delta>0 \\ S=-\frac{b}{a}\lt 0 \\ P=\frac{c}{a}>0\end{array}\right.\).
Một số bài toán về bất phương trình bậc hai thường gặp.
Cho tam thức bậc hai \(f(x)=a x^{2}+b x+c=0\) vói \(a \neq 0\).
1. \(f(x)\gt 0, \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{array}{l}a>0 \\ \Delta\lt 0\end{array}\right.\).
2. \(f(x) \geq 0, \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{array}{l}a>0 \\ \Delta \leq 0\end{array}\right.\).
3. \(f(x)\lt 0, \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{array}{l}a\lt 0 \\ \Delta\lt 0\end{array}\right.\).
4. \(f(x) \leq 0, \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{array}{l}a\lt 0 \\ \Delta \leq 0\end{array}\right.\).
VÍ DỤ MINH HỌA
Ví dụ 1. Cho hàm số \(y=\sqrt{x+\sqrt{1+x^{2}}}\). Chúmg minh rằng \(2 y \cdot \sqrt{1+x^{2}}-y=0\).
Ta có: \(y^{\prime}=\frac{u^{\prime}}{2 \sqrt{u}}=\frac{\left(x+\sqrt{1+x^{2}}\right)^{\prime}}{2 \sqrt{x+\sqrt{1+x^{2}}}}=\frac{1+\frac{x}{\sqrt{1+x^{2}}}}{2 \sqrt{x+\sqrt{1+x^{2}}}}=\frac{x+\sqrt{1+x^{2}}}{2 \sqrt{x+\sqrt{1+x^{2}}} \sqrt{1+x^{2}}}=\frac{\sqrt{x+\sqrt{1+x^{2}}}}{2 \sqrt{1+x^{2}}}\).
Do đó: \(2 y^{\prime} \cdot \sqrt{1+x^{2}}-y=2 \frac{\sqrt{1+\sqrt{1+x^{2}}}}{2 \sqrt{1+x^{2}}} \cdot \sqrt{1+x^{2}}-\sqrt{1+\sqrt{1+x^{2}}}=\sqrt{1+\sqrt{1+x^{2}}}-\sqrt{1+\sqrt{1+x^{2}}}=0\)
Vây \(2 y^{\prime} \cdot \sqrt{1+x^{2}}-y=0\).
Ví dụ 2. Cho hàm số \(y=3 x+\sqrt{10-x^{2}}\). Giai phương trình \(y^{\prime}=0\).
Điều kiện: \(-\sqrt{10} \leq x \leq \sqrt{10}\left({ }^{*}\right)\).
Ta có \(y^{\prime}=3-\frac{x}{\sqrt{10-x^{2}}}\).
Khi đó,
\[\begin{array}{l}y^{\prime}=0 \Leftrightarrow 3-\frac{x}{\sqrt{10-x^{2}}}=0 \Leftrightarrow 3 \sqrt{10-x^{2}}=x \Leftrightarrow\left\{\begin{array}{l}x \geq 0 \\9\left(10-x^{2}\right)=x^{2}\end{array}\right. \\\Leftrightarrow\left\{\begin{array} { l } { x \geq 0 } \\{ 1 0 x ^ { 2 } - 9 0 = 0 }\end{array} \Leftrightarrow \left\{\begin{array}{l}x \geq 0 \\x= \pm 3\end{array} \Leftrightarrow x=3\right.\right. \text {. } \\\end{array}\]Vậy phương trình \(y^{\prime}=0\) có nghiệm duy nhất \(x=3\).!
Cần nhớ \(: \sqrt{A}=B \Leftrightarrow\left\{\begin{array}{l}B \geq 0 \\ A=B^{2} .\end{array}\right.\)
Ví dụ 3. Cho hàm số \(y=\frac{x^{2}+5 x-2}{x-1}\). Giai bất phương trinh \(y^{\prime}\lt 0\).
Ta có \(y^{\prime}=\frac{x^{2}-2 x-3}{(x-1)^{2}}\).
Điều kiện \(x \neq 1\left({ }^{*}\right)\).
Khi đó \(y^{\prime}\lt 0 \Leftrightarrow x^{2}-2 x-3\lt 0 \Leftrightarrow-1\lt x\lt 3\).
Đối chiếu vói điều kiện (*), bất phương trinh \(y^{\prime}\lt 0\) có tập nghiệm là \(S=(-1 ; 3) \backslash\{1\}\).
Vídụ 4. Cho hàm số \(f(x)=\frac{1}{3}\left(m^{2}-m-6\right) x^{3}-(m+2) x^{2}-4 x+m\). Tïm tham số \(m\) sao cho \(f^{\prime}(x)\lt 0, \forall x \in \mathbb{R}\).
Ta có \(f^{\prime}(x)=\left(m^{2}-m-6\right) x^{2}-2(m+2) x-4\).
- TH1: \(m^{2}-m-6=0 \Leftrightarrow\left[\begin{array}{l}m=-2 \\ m=3\end{array}\right.\).
Nếu \(m=-2\) thì \(f^{\prime}(x)=-4\lt 0, \forall x \in \mathbb{R}\). Do đó, \(m=-2\) thóa mãn bài toán.
Nếu \(m=3\) thì \(f^{\prime}(x)=-10 x-4\lt 0\) là nhị thức bậc nhất nên \(f^{\prime}(x)\) không lón hơn 0 với mọi \(x \in \mathbb{R}\). Do đó, \(m=3\) không thóa mãn bài toán.
- TH2: \(m^{2}-m-6 \neq 0 \Leftrightarrow\left\{\begin{array}{l}m \neq-2 \\ m \neq 3\end{array}\right.\).
Khi đó: \(f^{\prime}(x)\lt 0, \forall x \in \mathbb{R} \Leftrightarrow\left(m^{2}-m-6\right) x^{2}-2(m+2) x-4\lt 0, \forall x \in \mathrm{R}\)\(\Leftrightarrow\left\{\begin{array}{l}a\lt 0 \\ \Delta^{\prime}\lt 0\end{array} \Leftrightarrow\left\{\begin{array}{l}m^{2}-m-6\lt 0 \\ (m+2)^{2}+4\left(m^{2}-m-6\right)\lt 0\end{array} \Leftrightarrow\left\{\begin{array}{l}m^{2}-m-6\lt 0 \\ 5 m^{2}-20\lt 0\end{array} \Leftrightarrow\left\{\begin{array}{l}-2\lt m\lt 3 \\ -2\lt m\lt 2\end{array} \Leftrightarrow-2\lt m\lt 2\right.\right.\right.\right.\).
Vậy, giá trị \(m\) cần tìm là \(-2 \leq m \leq 2\).
3.4 Bài toán tính đạo hàm hàm lượng giác
Bảng công thức đạo hàm lượng giác:
10. \((\sin x)^{\prime}=\cos x\) \((\sin u)^{\prime}=u^{\prime} \cdot \cos u\)
11. \((\cos x)^{\prime}=-\sin x\) \((\cos u)^{\prime}=-u^{\prime} \cdot \sin u\)
12. \((\tan x)^{\prime}=\frac{1}{\cos ^{2} x}=1+\tan ^{2} x\) \((\tan u)^{\prime}=\frac{u^{\prime}}{\cos ^{2} u}=u^{\prime}\left(1+\tan ^{2} u\right)\)
13. \((\cot x)^{\prime}=\frac{-1}{\sin ^{2} x}=-1\left(1+\cot ^{2} u\right)\) \((\cot u)^{\prime}=\frac{-u^{\prime}}{\sin ^{2} u}=-u^{\prime}\left(1+\cot ^{2} u\right)\)
14. \((\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}\) \((\arcsin u)^{\prime}=\frac{u^{\prime}}{\sqrt{1-u^{2}}}\)
15. \((\arccos x)^{\prime}=\frac{-1}{\sqrt{1-x^{2}}}\) \((\arccos u)^{\prime}=\frac{-u^{\prime}}{\sqrt{1-u^{2}}}\)
16. \((\arctan x)^{\prime}=\frac{1}{1+x^{2}}\) \((\arctan u)^{\prime}=\frac{u^{\prime}}{1+u^{2}}\)
17. \((\operatorname{arccot} x)^{\prime}=\frac{-1}{1+x^{2}}\) \((\operatorname{arccot} u)^{\prime}=\frac{-u^{\prime}}{1+u^{2}}\)
VÍ DỤ MINH HỌA
Tính đạo hàm của các hàm số sau:
1. \(y=5 \sin x-3 \cos x\). ĐS: \(y^{\prime}=5 \cos x+3 \sin x\).
2. \(y=x-\frac{9}{x}+\frac{2}{x^{4}+6 x^{3}-1}\). ĐS: \(y=1+\frac{9}{x^{2}}-\frac{2\left(4 x^{3}+18 x^{2}\right)}{\left(x^{4}+6 x^{3}-1\right)^{2}}\).
3. \(y=\cos ^{2} 5 x\). ĐS: \(y^{\prime}=-5 \sin 10 x\).
4. \(y=\tan ^{3}\left(5 x+\frac{\pi}{3}\right)\). ĐS: \(y=15 \cdot \tan ^{2}\left(5 x+\frac{\pi}{3}\right) \cdot \frac{1}{\cos ^{2}\left(5 x+\frac{\pi}{3}\right)}\).
3.5 Bài toán chứng minh đẳng thức, giải phương trình chứa đạo hàm
PHƯƠNG PHÁP:
- Tính đạo hàm của hàm số đã cho
- Thay \(y, y^{\prime}\) vào biểu thức để biến đổi chứng minh hoặc giải phương trình liên quan.
VÍ DỤ MINH HỌA
Ví dụ 1. Cho hàm số \(y=\tan x\). Chưng minh \(y^{\prime}-y^{2}-1=0\).
Điều kiện xác định của hàm số là \(x \neq \frac{\pi}{2}+k \pi, k \in Z\)
Ta có \(y^{\prime}=\frac{1}{\cos ^{2} x}=1+\tan ^{2} x\)
Khi đó \(y^{\prime}-y^{2}-1=1+\tan ^{2} x-\tan ^{2} x-1=0\)(đpcm)
Ví dụ 2. Cho hàm số \(f(x)=\sin 2 x-2 \cos x\). Giai phương trình \(f^{\prime}(x)=0\).
Ta có \(f^{\prime}(x)=2 \cos 2 x+2 \sin x\).
Khi đó \(f^{\prime}(x)=0 \Leftrightarrow 2 \cos 2 x+2 \sin x=0 \Leftrightarrow-2 \sin ^{2} x+\sin x+1=0\)
\[\Leftrightarrow\left[\begin{array} { l } { \operatorname { s i n } x = 1 } \\{ \operatorname { s i n } x = - \frac { 1 } { 2 } }\end{array} \left[\begin{array}{l}x=\frac{\pi}{2}+k 2 \pi, k \in Z \\x=-\frac{\pi}{6}+k 2 \pi, k \in Z . \\x=\frac{7 \pi}{6}+k 2 \pi, k \in Z\end{array}\right.\right.\]Vạy phương trình \(f^{\prime}(x)=0\) có các nghiệm \(x=\frac{\pi}{2}+k 2 \pi, x=-\frac{\pi}{6}+k 2 \pi, x=\frac{7 \pi}{6}+k 2 \pi\) vơi \(k \in Z\).
4. Bài tập ứng dụng của đạo hàm
4.1 Cực trị và khoảng tăng giảm
TÌM CỰC TRỊ CỦA HÀM SỐ
Định nghĩa
Hàm số \(y=f(x)\) xác định và liên tục trong lân cận \(\left(x_{0}-\varepsilon, x_{0}+\varepsilon\right)\) của điếm \(x_{0}\), khi đó vói mọi \(x \in\left(x_{0}-\varepsilon, x_{0}+\varepsilon\right)\)
Giá trị của hàm \(f\) trong lân cận điểm \(x_{0}\) Kết luận về hàm \(f\) tại điểm \(x_{0}\)
\(f(x) \leq f\left(x_{0}\right)\) \(x_{0}\) là điểm cực đại và \(f_{C D}=f\left(x_{0}\right)\)
\(f(x) \geq f\left(x_{0}\right)\) \(x_{0}\) là điểm cực tiểu và \(f_{C T}=f\left(x_{0}\right)\) Điểm cực đại và điểm cực tiếu được gọi chung là diểm cưc trị của hàm số.\(f_{C D}, f_{C T}\) : gọi chung là cưc trị hàm số.
- TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Hàm số \(y=f(x)\) giảm trên khoảng \((a, b)\) nếu \(x_{1}\lt x_{2}\) thì \(f\left(x_{1}\right)\gt f\left(x_{2}\right)\) với mọi \(x_{1}, x_{2} \in(a, b)\).
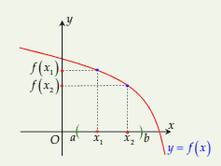
Hàm số \(y=f(x)\) tăng trên khoảng \((a, b)\) nếu \(x_{1}\lt x_{2}\) thì \(f\left(x_{1}\right)\lt f\left(x_{2}\right)\) với mọi \(x_{1}, x_{2} \in(a, b)\).
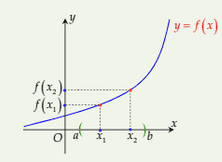
Cho hàm số \(y=f(x)\) có đạo hàm trên khoảng \((a, b)\).
\(y^{\prime}=f^{\prime}(x)\) Kết luận về hàm \(f\) trên khoảng \((a, b)\)
\(f^{\prime}(x)\gt 0, \forall x \in(a, b)\) Tăng
\(f^{\prime}(x) \geq 0, \forall x \in(a, b)\) Không giảm
\(f^{\prime}(x)\lt 0, \forall x \in(a, b)\) Giảm
\(f^{\prime}(x) \leq 0, \forall x \in(a, b)\) Không tăn
Phương pháp tìm cực trị, khoảng tăng giảm
Cho hàm số \(y=f(x)\) có đạo hàm trên tập xác định \(D\) (có thế trừ ra hữu hạn điểm). Đế khảo sát tính đơn điệu và tìm cưc trị của \(f(x)\) ta tiến hành các bước sau:
Bước 1. Tính đạo hàm \(y^{\prime}=f^{\prime}(x)\).
Bước 2. Tìm tất cả các điểm tới hạn \(x_{1}, x_{2}, \ldots, x_{n} \in D\).(điểm tới hạn là điểm mà tại đó \(f^{\prime}(x)=0\) hoặc \(f^{\prime}(x)\) không xác định)
Bước 3. Lập bảng biến thiên, xét dấu đạo hàm
Cách 1. Lập bảng biến thiên, xét dấu đạo hàm \(f^{\prime}(x)\).
Cách 2. Dùng đạo hàm cấp 2- \(\left\{\begin{array}{l}f^{\prime}\left(x_{0}\right)=0 \\ f^{\prime \prime}\left(x_{0}\right)\gt 0\end{array} \longrightarrow f\right.\) đạt cưc tiểu tại điểm \(x_{0}\).- \(\left\{\begin{array}{l}f^{\prime}\left(x_{0}\right)=0 \\ f^{\prime \prime}\left(x_{0}\right)\lt 0\end{array} \Longrightarrow f\right.\) đạt cưc đại tại điểm \(x_{0}\).
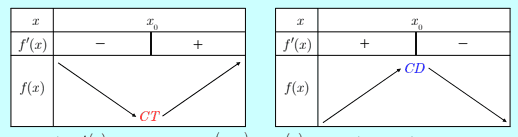
\(\checkmark\) Nếu \(f^{\prime}(x)\gt 0\) trên khoảng \((a, b)\) thì \(f(x)\) tăng (đồng biến) trên khoảng đó.
\(\checkmark\) Nếu \(f^{\prime}(x)\lt 0\) trên khoảng \((a, b)\) thì \(f(x)\) giảm (nghịch biến) trên khoảng đó.
\(\checkmark\) Nếu \(f^{\prime}(x)\) đối dấu từ âm sang durong khi \(x\) vươt qua \(x_{0}\) thì \(f(x)\) đạt cực tiểu tại \(x_{0}\).
\(\checkmark\) Nếu \(f^{\prime}(x)\) đối dấu từ duơng sang âm khi \(x\) vượt qua \(x_{0}\) thì \(f(x)\) đạt cực đại tại \(x_{0}\).
- BÀI TẬP ỨNG DỤNG
Ví dụ 1 Khảo sát tính đơn điệu và tìm cực trị hàm số \(y=x^{4}-4 x^{3}+5\).
Bài giải
\(\checkmark\) Miên xác định \(D=\mathbb{R}\).\(\checkmark\) Ta có \(y^{\prime}=4 x^{3}-12 x^{2}=4 x^{2}(x-3)\).Do đó \(\quad y^{\prime}=0\)
\[\Leftrightarrow 4 x^{2}(x-3)=0 \Leftrightarrow x=0 \vee x=3 .\]\(\checkmark\) Bảng biến thiên
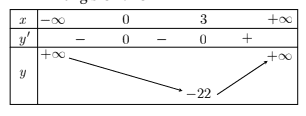
Vậy
- \(y\) giảm trên \((-\infty, 3)\) và \(y\) tăng trên \((3,+\infty)\).
- \(y\) đạt cực tiểu tại \(x=3\) với
\[y_{c T}=y(3)=-22 .\]Ví dụ 2 Khảo sát tính đơn điệu và tìm cực trị hàm số \(y=\frac{x^{2}-3}{x^{3}}\).
Bài giải
\(\checkmark\) Miền xác định \(D=\mathbb{R} \backslash\{0\}\).
\(\checkmark\) Ta có \(y^{\prime}=\frac{2 x \cdot x^{3}-3 x^{2}\left(x^{2}-3\right)}{\left(x^{3}\right)^{2}}\)
\[\begin{array}{l}=\frac{2 x^{4}-3 x^{4}+9 x^{2}}{x^{6}} \\=\frac{9-x^{2}}{x^{4}} .\end{array}\]Do đó \(\quad y^{\prime}=0 \Leftrightarrow 9-x^{2}=0\)
\[\Leftrightarrow x=3 \vee x=-3 \text {. }\]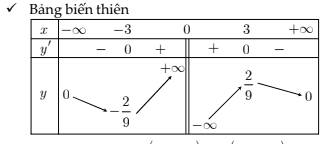
Vậy
- \(y\) giảm trên \((-\infty, 3)\) và \((3,+\infty)\), \(y\) tăng trên \((-3,0)\) và \((0,3)\).
- \(y\) đạt cực tiểu tại \(x=-3\) với \(y_{C T}=y(-3)=-\frac{2}{9}\) và đạt cực đại tại \(\dot{x} \cdot 3\) với \(y_{C D}=y(3)=\frac{2}{9}\).
4.2 Giá trị lớn nhất và giá trị nhỏ nhất
GIÁ TRỊ LỚN NHẤT GIÁ TRỊ NHỎ NHẤT
Định nghĩa:
Cho hàm số \(y=f(x)\) xác định trên tập \(D\).
\(\checkmark\) Số \(M\) được gọi là giá trị lón nhất của hàm số \(y=f(x)\) trên \(D\) nếu
\[\left\{\begin{array}{l}\forall x \in D: f(x) \leq M \\\exists x_{1} \in D: f\left(x_{1}\right)=M\end{array}\right.\]Ký hiệu: \(M=\max _{D} f(x)\)
\(\checkmark\) Số m được gọi là giá trị nhỏ nhất của hàm số \(y=f(x)\) trên \(D\) nếu
\[\left\{\begin{array}{l}\forall x \in D: f(x) \geq m \\\exists x_{2} \in D: f\left(x_{2}\right)=m\end{array}\right.\]Ký hiệu: \(m=\min _{D} f(x)\)
\(\checkmark\) Đoạn \([m, M]\) gọi là miền giá trị của hàm số \(y=f(x)\).
Phương pháp giải GTLN & GTNN của hàm số trên đoạn [a;b]
Bước 1. Tính đạo hàm \(y^{\prime}=f^{\prime}(x)\) rồi suy ra các điểm tới hạn \(x_{1}, x_{2}, \ldots\) của hàm số \(y=f(x)\) trên \([a, b]\).
Bước 2. Tính giá trị \(f(a), f(b), f\left(x_{1}\right), f\left(x_{2}\right), \ldots\)
Bước 3. So sánh tất cả các giá trị đó ta suy ra được GTLN & GTNN.
Chú ý
Để tìm GTLN và GTNN của \(y=f(x)\) trên các khoảng hay nửa khoảng ta cần phải lập bảng biến thiên.
- BÀI TẬP ỨNG DỤNG
Ví dụ : Tìm GTLN & GTNN của hàm số \(y=3 x^{4}-28 x^{3}+90 x^{2}-108 x+1\) trên đoạn \([0,4]\).
Bài giải
Ta có \(\quad y^{\prime}=12 x^{3}-84 x^{2}+180 x-108\).
Do đó \(\quad y^{\prime}=0\)
\[\begin{array}{l}\Leftrightarrow 12 x^{3}-84 x^{2}+180 x-108=0 \\\Leftrightarrow\left[\begin{array}{l}x=1 \in[0,4] \\x=3 \in[0,4]\end{array} .\right.\end{array}\]\[\begin{array}{ll}y(0)=1, & y(1)=-42, \\y(3)=-26, & y(4)=-15 .\end{array}\]Vậy \(\quad \max _{0,4} y(x)=y(0)=1\)
và \(\min _{[0,4]} y(x)=y(1)=-42\).
4.3 Ứng dụng của đạo hàm vào thực tế
- CÁC BÀI TOÁN ỨNG DỤNG ĐẠO HÀM TRONG THỰC TẾ
Bước 1: Dưa trên các giả thiết và yếu tố của đề bài, ta xây dưng mô hình Toán học cho vấn đề đang xét, tức là diễn tả "duới dạng ngôn ngũ Toán học" cho mô hinh mô phōng thực tiển.
Lưu ý là ứng với vấn đề đươc xem xét có thể có nhiều mô hình toán học khác nhau, tùy theo các yếu tố nào của hệ thống và mối liên hệ giữa chúng đuợc xem là quan trọng ta đi đến việc biểu diễn chúng duó̃i dạng các biến số, tìm các điều kiện tồn tại của chúng cũng như sự ràng buộc, liên hệ với các giả thiết của đề bài.
Bước 2: Dựa vào các kiến thức liên quan đến vấn đề thực tế như trong kinh tế, đời sống, trong khoa học kỹ thuật nhnhư Vật lý, Hóa học, Sinh học,... Ta thiết lập hoàn chinh hàm số phụ thuộc theo một biến hoăc nhiểu biến. (Ở đây trong nội dung đang xét ta chi xét với tính huống 1 biến).
Bước 3: Sử dụng công cụ đạo hàm của hàm số để khảo sát và giái quyết bài toán hình thành ở bước 2. Luu ý các điều kiện ràng buộc củcủa biến số và kết quà thu được có phù hợp với bài toán thực tế đã cho chưa.
- BÀI TẬP ỨNG DỤNG
- Trong Hinh học (bài toán 1 và bài toán 2 ).
- Trong Vật lý (bài toán 3 và bài toán 4).
- Trong Kinh tế (bài toán 5 và bài toán 6).
- Trong Đời sống và các lĩnh vục khác (bài toán 7 và bài toán 8 ).
Bài toán 1. Từ một tấm tôn hình chữ nhật có kích thước là \(a^{\prime} b\) với \(a\lt b\). Người ta cắt bỏ 4 hình vuông bằng nhau ở 4 góc rồi gò thành một hình hộp chữ nhật không có nắp. Hỏi cạnh của hình vuông cắt đi phải bằng bao nhiêu để hình hộp đó có thể tích lớn nhất ?
Phân tích:
- Trước tiên, với câu hỏi của bài toán thì ta nên đặ̆t x chính là cạnh của hình vuông cắt đi. Nhe vậy ta cần tìm điều kiện giới hạn cuia biến số \(\mathrm{x}\). Do khi đó I cạnh của tấm nhôm sau khi bị cắt trở thành \(\mathrm{a}-2 \mathrm{x}\gt 0 \Rightarrow \mathrm{x}\lt \frac{\mathrm{a}}{2}\) nên ta có \(0\lt \mathrm{x}\lt \frac{\mathrm{a}}{2}\).
- Và đồng thời ta cũng có đurơc cạnh cuia tấm nhôm còn lại là \(\mathrm{b}-2 \mathrm{x}\gt 0\). Đến đây ta cần thiết lập công thức tinh thể tich khối hôp \(V=x(a-2 x)(b-2 x)\)
- Bài toán trở thành tìm \(\max _{x \in\left(0 ; \frac{a}{2}\right)} V(x)=?\) Mời bạn đọc xem lời giải.
Huớng dẫn giải.
- Gọi \(x\) là cạnh của hình vuông cắt đi, ta phải có điều kiện \(0\lt x\lt \frac{a}{2}\).
Khi đó thể tích hình hộp là \(V=x(a-2 x)(b-2 x)=4 x^{3}-2(a+b) x^{2}+a b x=V(x)\).
- Bài toán trở thành tìm \(\max _{x \in\left(0, \frac{\pi}{2}\right)} V(x)=\) ?
Đạo hàm \(V^{\prime}=f^{\prime}(x)=12 x^{2}-4(a+b) x+a b\).
Ta có \(\Delta^{\prime}=4(a+b)^{2}-12 a b=4\left(a^{2}-a b+b^{2}\right)\gt 0\) với mọi \(a, b\).
Do đó \(V^{\prime}=0\) luôn có hai nghiệm phân biệt
\[\begin{array}{c}x_{1}=\frac{a+b-\sqrt{a^{2}-a b+b^{2}}}{6}\lt x_{2}=\frac{a+b+\sqrt{a^{2}-a b+b^{2}}}{6} \\\text { Theo định lý Vi-et, ta có }\left\{\begin{array}{l}x_{1}+x_{2}=\frac{a+b}{3}\gt 0 \\x_{1} x_{2}=\frac{a b}{12}>0\end{array}\right.\end{array}\]suy ra \(0\lt x_{1}\lt x_{2}\).
Hơn nữa, ta có \(V^{\prime}\left(\frac{a}{2}\right)=f^{\prime}\left(\frac{a}{2}\right)=a^{2}-a b=a(a-b)\lt 0\). Do đó \(0\lt x_{1}\lt \frac{a}{2}\lt x_{2}\).
Bảng biến thiên
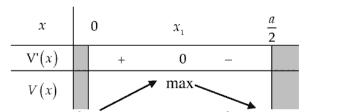
- Dự vào bảng biến thiên ta thấy \(V\) đạt giá trị lớn nhất khi
\[x=x_{1}=\frac{a+b-\sqrt{a^{2}-a b+b^{2}}}{6} \text {. }\]Bài toán 2. Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích \(V\left(\mathrm{~m}^{3}\right)\) không đổi, hệ số \(k\gt 0\) cho trước ( \(k\) là tỉ số giứa chiều cao của hố và chiều rộng của đáy. Hãy xác định các kích thước của đáy để khi xây tiết kiệm nguyên vật liệu nhất?
Phân tích:
- Với thể tich V cho trước và quan hệ giữa chiều rông cuia đáy và chiều cao của hình hộp ta hoàn toàn có thể biểu diễn được độ dài chiều dài theo 1 biến.
- Như vậy ta cần hiểu yêu cầu bài toán "tiết kiệm nguyên vật liệu nhất là gì ?" Đó chính là làm sao cho phần bao phủ bên ngoài hình hộp có diện tich nhỏ nhất hay diện tích toàn phần cuia khối hộp nhỏ nhất.
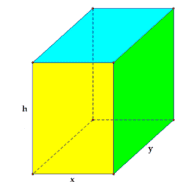
Hướng dẫn giải:
- Gọi \(x, y(0\lt x\lt y)\) lần lượt là chiều rộng và chiều dài của đáy hố ga.
Gọi \(h\) là chiều cao của hố ga \((h\gt 0)\).
- Theo đề bài ta có \(h=k x\) và \(V=h x y \Rightarrow y=\frac{V}{h x}=\frac{V}{k x^{2}}\)
Để tiết kiệm nguyên vật liệu nhất ta cần tìm các kich thước sao cho diện tích toàn phần của hố ga là nhô nhất.
Khi đó ta có: \(S_{t p}=2 x h+2 y h+2 x y=2 x(k x)+2(k x) \cdot \frac{V}{k x^{2}}+2 x \frac{V}{k x^{2}}\)
Suy ra \(S_{t p}=2 k x^{2}+\frac{2\left(\frac{k+1}{k}\right) V}{x}\) Xét hàm số \(f(x)=2 k x^{2}+\frac{2\left(\frac{k+1}{k}\right) V}{x}\).
Bài toán trở thành tìm giá trị nhỏ nhất của \(f(x)\) với \(x\gt 0\).
\[f^{\prime}(x)=4 k x-\frac{2\left(\frac{k+1}{k}\right) V}{x^{2}}=2 \frac{2 k^{2} x^{3}-(k+1) V}{k x^{2}}, \text { cho } f^{\prime}(x)=0 \Leftrightarrow x_{o}=\sqrt[3]{\frac{(k+1) V}{2 k^{2}}}>0\]Lập bảng biến thiên ta có
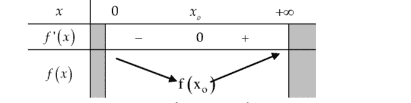
Dựa vào bảng biến thiên ta có \(\min _{x>0} f(x)=f\left(\sqrt[3]{\frac{(k+1) V}{2 k^{2}}}\right)\).
Khi đó \(y=\sqrt[3]{\frac{4 k V}{(k+1)^{2}}}\) và \(h=\sqrt[3]{\frac{k(k+1) V}{2}}\).
Bài toán 3. Một chất điểm chuyển động theo quy luật \(s(t)=6 t^{2}-t^{3}-9 t+1, \mathrm{~s}\) tính theo mét, \(\mathrm{t}\) tính theo giây. Trong 5 giây đầu tiên, thời điểm \(\mathrm{t}\) mà tại đó vận tốc của chuyển động đạt giá trị lớn nhất là:
A. \(t=3\).
B. \(t=1\).
C. \(t=2\).
D. \(t=4\).
Phân tích:
- Với kiến thức Vật lý đã học, ta biết \(\mathrm{v}(\mathrm{t})=\mathrm{s}^{\prime}(\mathrm{t})\). Do đó để tìm giá trị lớn nhất trong 5 giây đầu tiên \(\mathrm{t} \in[0 ; 5]\) thi ta chi cần vận dụng kiến thức đạo hàm đã học.
Huớng dẫn giäi
\[v(t)=s^{\prime}(t)=12 t-3 t^{2}-9, v^{\prime}(t)=-6 t+12, v^{\prime}(t)=0 \Leftrightarrow t=2 \text {. }\]Lập bảng biến thiên ta có:
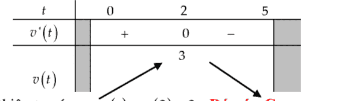
Dựa vào bảng biến thiên ta có \(\max _{\mathrm{t} \in(0 ; 5)} \mathrm{v}(\mathrm{t})=\mathrm{v}(2)=3\).. Đáp án \(C\).
Bài toán 4. Một nguồn điện với suất điện động \(E\) và điện trở \(r\) được nối với một biến trờ \(R\) như hình vẽ. Với giá trị nào của biến trờ thì công suất tỏa nhiệt trên toàn mạch sẽ đạt cực đại ?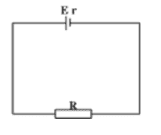
A. \(r=R\).
B. \(r=2 R\).
C. \(r=3 R\).
D. \(r=4 R\).
Phân tích:
- Để làm đượđược dang toán này, trước tiên ta cần có kiến thúc về dòng điện 1 chiều đãa học ờ lớp duoơit: công suất tòa nhiệt trên toàn mạch sẽ là \(P=R I^{2}\) và đồng thời cuờng âộ dòng điện trong mach sẽ là \(I=\frac{E}{R+r}\).
- Đến đây ta thấy \(P\) có thể tính theo \(R\) và r. Và do đó ta có thể vận dụng kiến thúc về đạo hàm để tìm giá trị lớn nhất, nhỏ nhất cùa biểu thúc P.
Hướng dẫn giải:
Theo công thức công suất tỏa nhiệt ta có \(P=R I^{2}\) với \(I=\frac{E}{R+r}\)
\(\Rightarrow P=\frac{R E^{2}}{(R+r)^{2}}(R\gt 0)\). Xét hàm số \(f(R)=\frac{R E^{2}}{(R+r)^{2}}\) với \(R>0\)
Ta tìm \(f^{\prime}(R)=E^{2} \frac{(R+r)^{2}-2 R(R+r)}{(R+r)^{4}}=E^{2} \frac{r-R}{(R+r)^{3}}, f^{\prime}(R)=0 \Leftrightarrow r=R\)
Lập bảng biến thiên ta có:
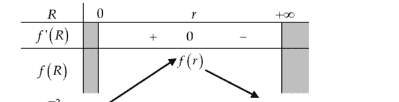
suy ra \(\max f(R)=f(r)=\frac{E^{2}}{4 r}\). Ta chọn đáp án A.
Bài toán 5. Một công ty đánh giá rằng sẽ bán được \(N\) lô hàng nếu tiêu phí hết số tiền là \(x\) (triệu đồng) vào việc quảng cáo. Biết rằng \(N\) và \(x\) liên hệ với nhau bằng biểu thức \(N(x)=-x^{2}+30 x+6,0 \leq x \leq 30\). Hãy tìm số lô hàng lớn nhất mà công ty có thể bán sau đợt quảng cáo và số tiền đã dành cho việc quảng cao đó ?
Huớng dẫn giải.
Ta có: \(N(x)=-x^{2}+30 x+6 \Rightarrow N^{\prime}(x)=-2 x+30 \Rightarrow N^{\prime}(x)=0 \Leftrightarrow x=15\)Đồng thời \(\left\{\begin{array}{l}N(0)=6 \\ N(15)=231 \\ N(30)=6\end{array} \Rightarrow \max _{x \in[0 ; 30]} N(x)=231 \Leftrightarrow x=15\right.\).
Vậy, nếu công ty dành 15 triệu cho việc quảng cáo thì công ty sẽ bán được nhiều nhất là 231 lô hàng.
Bài toán 6: Một công ty nhận sản xuất 400.000 huy chương bạc nhân ngày kỷ niệm lần thứ 30 Apollo 11 đổ bô lên mặt Trăng. Công ty sở hữu 20 máy, mỗi máy có thể sản xuất 200 huy chương/giờ.
Chi phí lắp đặt máy để sản xuất huy chương là 80 USD/máy và tổng chi phí vận hành là 5,76 USD/giờ. Hãy biểu diễn chi phí sản xuât 400.000 huy chương bằng một hàm theo số máy đã dùng. Hãy uớc tính số máy mà công ty nên dùng đề chi phí nhỏ nhất.
Hướng dẫn giải
Gọi \(x(1 \leq x \leq 20, x \in \square)\) là số máy sử dụng và \(C(x)\) là hàm tổng chi phí sản xuất tương ứng.
Chi phí lắp đặt các máy là \(80 x\)
Chi phí vận hành các máy là \(\frac{400000}{200 x} \cdot 5,76\)
Tổng chi phí \(=\) Chi phí lắp đặt + Chi phí vận hành \(\Rightarrow C(x)=80 x+\frac{11520}{x}\)
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số \(C(x)\) với \(x \in[1 ; 20]\)
Ta có \(C^{\prime}(x)=80-\frac{11520}{x^{2}} \Rightarrow C^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=12(\mathrm{tm}) \\ x=-12(\mathrm{ktm})\end{array}\right.\)
Đồng thời \(\left\{\begin{array}{l}C(1)=11600 \\ C(20)=2176 \\ C(12)=1920\end{array} \Rightarrow \max _{x \in[1: 20]} C(x)=C(12)=1920 \Leftrightarrow x=12\right.\)
Vậy công ty nên sử dụng 12 máy để sản xuất thì tổng chi phí sẽ nhỏ nhất.
Bài toán 7 (Ứng dụng trong Sinh học). Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định được số lượng vi khuẩn tăng theo thời gian bởi qui luật \(N(t)=1000+\frac{100 t}{100+t^{2}}\) (con vi khuẩn), trong đó \(t\) là thời gian (đơn vị giây)). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào, số lượng vi khuẩn tăng lên là lớn nhất ?
Phân tích:
- Tương tự như những bài toán truớc, do đề bài đã mô hình hóa bài toán durới dạng hàm nên ta chi cần vận dụng kiến thức đạo hàm là có thể tìm được số lượng tăng nhanh nhất cuia vi khuẩn.
Huớng dẫn giải
Ta có tốc độ phát triển của đàn vi khuẩn tại thời điểm \(t\) là
\[N^{\prime}(t)=\frac{100\left(100+t^{2}\right)-100 t(2 t)}{\left(100+t^{2}\right)^{2}}=\frac{100^{2}-100 t^{2}}{\left(100+t^{2}\right)^{2}}(\forall t\gt 0)\]Xét \(N^{\prime}(t)=0 \Leftrightarrow t^{2}=100 \Leftrightarrow t=10>0\).
Lâp bảng biến thiên ta được:
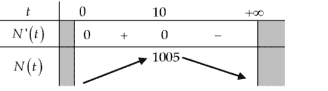
Dựa vào bảng biến thiên, ta kết luận \(\max N(t)=N(10)=1005\).
Bài toán 8 (Ứng dụng trong Y Học). Độ giảm huyết áp của bệnh nhân được cho bời công thức \(G(x)=0,025 x^{2}(30-x)\) với \(x\) là liều lượng thuốc được tiêm cho bệnh nhân ( \(x:\) miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm?
Phân tích:
- Tương tự như những bài toán đã cho sã̃n hàm số, thì việc ứng dụng đạo hàm không còn quá khó khăn nữa.
Huớng dẫn giải.
\[G(x)=\frac{1}{40} x^{2}(30-x)=\frac{1}{40}\left(30 x^{2}-x^{3}\right) \Rightarrow G^{\prime}(x)=\frac{1}{40}\left(60 x-3 x^{2}\right)\]Cho \(G^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=20 \\ x=0(k t m)\end{array}\right.\)
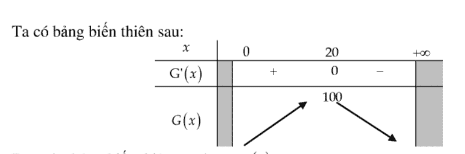
Dựa vào bảng biến thiên ta có \(\max G(x)=100 \Leftrightarrow x=20\).
5. Học đạo hàm hiệu quả bằng cách nào?
Sau đây là những cách mà Examon tích lũy từ kinh nghiệm cá nhân khi học đạo hàm và muốn giới thiệu đến các bạn học sinh:
- Học phải hiểu bản chất của đạo hàm: Nắm vững định nghĩa và ghi nhớ các công thức của đạo hàm.
- Thường xuyên làm bài tập: Thực hành các bài tập đạo hàm đa dạng để củng cố kiến thức
- Áp dụng vào thưc tế: tìm hiểu những ứng dụng trong các bài toán thực tế để hiểu sâu hơn về Đạo hàm
- Sử dụng tài liệu bổ trợ: Tìm nguồn tài liệu uy tín, video có hướng dẫn bài tập để bổ sung thêm kiến thức
- Tìm phương pháp học hiệu quả: Đây là lời khuyên quan trọng nhất, việc tìm kiếm một phương pháp học hiệu quả vô cùng quan trọng bởi có một phương phap học hiệu quả như là đã hoàn thành được 30% kiến thức, có phương pháp học để bạn không đi sai hướng, có lộ trình đầy đủ. Examon đã tìm được một phương pháp học để bạn có thể theo đúng lộ trình của kiến thức, bạn hãy cùng Examon tìm hiểu nhé!
PHƯƠNG PHÁP "LUYỆN ĐỀ" CÙNG EXAMON
Đã bao giờ bạn tự hỏi tại sao việc luyện đề lại quan trọng đến vậy không? Rất nhiều bạn đã mắc sai lầm nghiêm trọng khi luyện đề: Không phải mọi bộ đề đều giống nhau.
Nhiều bạn vẫn thường tìm kiếm và làm những bộ đề cũ kỹ, lỗi thời trên mạng mà không biết rằng chúng có thể không phản ánh chính xác chương trình học hay xu hướng ra đề mới nhất. Điều này không chỉ khiến bạn mất thời gian mà còn có thể dẫn đến những hiểu lầm về năng lực thực sự của mình.

Luyện đề đúng cách là phương pháp để bạn có thể nhận diện các dạng bài tập thường gặp, nắm vững phương pháp giải quyết hiệu quả và từ đó, nâng cao kỹ năng giải đề của mình. Với hệ thống đề được cập nhật liên tục và chính xác, Examon sẽ giúp bạn:
- Nhận diện các dạng bài thi quan trọng.
- Luyện tập với các phương pháp làm bài tối ưu.
- Thành thạo kỹ năng giải đề, sẵn sàng cho mọi kỳ thi.
Dưới đây, Examon sẽ hướng dẫn bạn cách luyện đề hiệu quả với hệ thống đề của Examon:
- Bước 1: Tạo và Đăng nhập tài khoản Đầu tiên, các bạn cần có một tài khoản Examon. Chỉ với vài thao tác đăng ký nhanh chóng, bạn đã sẵn sàng cho hành trình chinh phục kiến thức!
- Bước 2: Tiếp theo, hãy chọn lớp học, môn học mà bạn muốn luyện và khu vực bạn đang sống để Examon cung cấp đề thi phù hợp nhất với bạn.
- Bước 3: Lựa chọn đề thi và Bắt đầu luyện, Examon có hai chế độ: Luyện tập để bạn làm quen và Thi thử để kiểm tra năng lực. Hãy chọn một đề thi phù hợp và bắt đầu luyện!
- Bước 4: Khi làm bài, hãy tập trung và nghiêm túc như thể bạn đang ở trong phòng thi thật sự. Đây là cơ hội để rèn luyện sự tự tin và kỹ năng giải quyết vấn đề của bạn.
- Bước 5: Nhận điểm và Phân tích kết quả sau khi hoàn thành, bạn sẽ nhận được điểm số ngay lập tức cùng với lời giải chi tiết cho từng câu hỏi, giúp bạn hiểu rõ mình cần cải thiện ở đâu.
Tham khảo ngay bộ đề được biên soạn đặc biệt bám sát 99,9% đề tham khảo kỳ thi THPT năm 2024 của Examon ngay!