Tích phân hàm chứa dấu trị tuyệt đối

Cho \(f(x)\) là hàm số liên tục trên đoạn \([a ; b]\). 

Giả sử \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([a ; b]\).

Hiệu số \(F(a)-F(b)\) được gọi là tích phân từ \(a\) đến \(b\) của hàm số \(f(x)\), kí hiệu là

trong đó : 

\(\int\) là dấu tích phân

\(a\) là cận dưới, \(b\) là cận trên

\(f(x) \mathrm{d} x\) là biểu thức dưới dấu tích phân

\(f(x)\) là hàm số dưới dấu tích phân.

Đặt vấn đề : Tính \(\int_{a}^{b} g(x) d x\) trong đó \(g(x)\) là biểu thức chứa ẩn trong dấu giá trị tuyệt đối

Phương pháp giải :

Muốn tính tích phân \(I=\int_{a}^{b}|g(x)| d x\), ta thực hiện theo các bước sau:

+ Xét dấu hàm \(g(x)\) trên đoạn \([a ; b]\) để mở dấu giá trị tuyệt đối.

+ Áp dụng công thức ta có : \(\int_{a}^{b}|g(x)| d x=\int_{a}^{c}|g(x)| d x+\int_{c}^{b}|g(x)| d x\).

+ Tính mỗi tích phân thành phần

Ví dụ : Tính \(I=\int_{0}^{3}|1-x| d x\)

Lời giải:

Lập bảng xét dấu cho hàm số \(|1-x|\) trên đoạn \([0,3]\) với chú ý \(1-x=0 \Leftrightarrow x=1\)

Ta có :

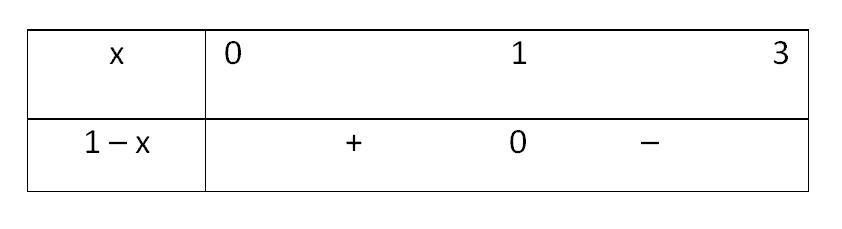
\(\begin{aligned} I & =\int_{0}^{1}|1-x| d x+\int_{1}^{3}|1-x| d x=\int_{0}^{1}(1-x) d x+\int_{1}^{3}(x-1) d x \\ & =\left.\left(x-\frac{x^{2}}{2}\right)\right|_{0} ^{1}+\left.\left(\frac{x^{2}}{2}-x\right)\right|_{1} ^{3}=\frac{1}{2}+2=\frac{5}{2}\end{aligned}\)

Tính chất 1: Nếu \(g{\left( x \right )} \ge 0\) với \(\forall x \in \left[ a , b \right ] \Rightarrow \int_{a}^{b} \left \lvert g{\left( x \right )} \right \rvert dx \ge 0\)

Ví dụ : Tính tích phân sau : \(\int_{1}^{2}|x-1| d x\)

 \(\begin{array}{l}\int_{1}^{2}|x-1| d x \\ \quad=\int_{1}^{2}(x-1) d x \\ \quad=\left.\left(\frac{x^{2}}{2}-x\right)\right|_{1} ^{2}=\frac{1}{2}\end{array}\)

Tính chất 2: Nếu \(g(x) \geq f(x)\) với \(\forall x \in[a, b]\) \(\Rightarrow \int_{a}^{b} g(x) d x \geq \int_{a}^{b} f(x) d x\)

Tính chất 3: \(\int_{a}^{b} g(x) d x=\int_{a}^{c}g(x) d x+\int_{c}^{b} g(x) d x\)

Ví dụ : Tính \(I=\int_{-2}^{4}\left|x^{2}-4 x+3\right| d x\)

Lời giải:

Lập bảng xét dấu cho hàm số \(\left|x^{2}-4 x+3\right|\) trên đoạn \([-1,4]\) với chú ý \(x^{2}-4 x+3=0 \Leftrightarrow\left[\begin{array}{l}x=1 \\ x=3\end{array}\right.\), 

Ta có : 

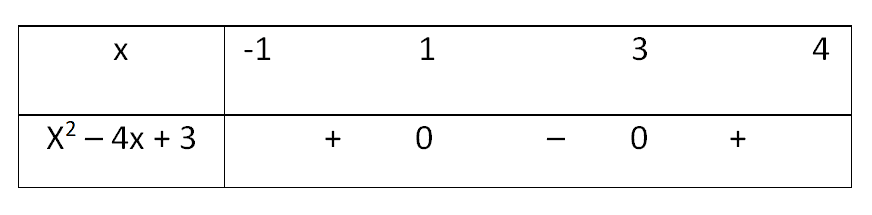
Do đó

\(I=\int_{-1}^{1}\left|x^{2}-4 x+3\right| d x+\int_{1}^{3}\left|x^{2}-4 x+3\right| d x+\int_{3}^{4}\left|x^{2}-4 x+3\right| d x\)

\(= \int_{-1}^{1}\left(x^{2}-4 x+3\right) d x- \int_{1}^{3}\left(x^{2}-4 x+3\right) d x+\int_{3}^{4}\left(x^{2}-4 x+3\right) d x\)

\(=\left.\left(\frac{x^{3}}{3}-2 x^{2}+3 x\right)\right|_{-1} ^{1}-\left.\left(\frac{x^{3}}{3}-2 x^{2}+3 x\right)\right|_{1} ^{3}+\left.\left(\frac{x^{3}}{3}-2 x^{2}+3 x\right)\right|_{3} ^{4}\)

\(=\frac{20}{3}+\frac{4}{3}+\frac{4}{3}\)

\(=\frac{28}{3}\)

Kết thúc bài viết này, Examon đã cùng nhau bạn khám phá và tìm hiểu về tích phân của các hàm chứa dấu giá trị tuyệt đối – một chủ đề thú vị và đầy thách thức trong toán học. Việc hiểu rõ và thành thạo các phương pháp giải tích phân với hàm chứa dấu giá trị tuyệt đối không chỉ giúp chúng ta nắm vững nền tảng lý thuyết mà còn mở ra nhiều ứng dụng thực tiễn trong đời sống và khoa học. 

Hy vọng rằng qua bài viết này, các bạn học sinh sẽ cảm thấy tự tin hơn khi đối mặt với các bài toán tích phân phức tạp, từ đó phát triển tư duy toán học và khả năng giải quyết vấn đề một cách hiệu quả hơn. Chúng ta sẽ luôn thấy rằng, qua mỗi thử thách, sự trưởng thành và kiến thức thu được sẽ là hành trang quý báu trên con đường học tập và nghiên cứu sau này.

Việc đi học thêm 1 lớp có 30 học sinh nhưng chỉ học duy nhất 1 bộ giáo trình là khó cho giáo viên vì mỗi học sinh đều có 1 năng lực khác nhau có học sinh giỏi TÍCH PHÂN yếu XÁC SUẤT như vậy học sinh đi học thêm sẽ mất cả X2 thời gian là điều không cần thiết, thay vì mình dùng ½ time tiết kiệm luyện thêm 1 phần VECTƠ giúp học sinh rút ngắn thời gian luyện tập và tăng hiệu quả học.

Với nỗi băn khoăn ấy đội ngũ founder Examon đã xây dựng nên 1 sản phẩm hỗ trợ học hiệu quả và cá nhân hóa việc học đến từng năng lực học sinh, cùng với sự hỗ trợ Gia sư AI sẽ giúp hs có trải nghiệm học tức thì và cải thiện ĐIỂM SỐ nhanh 200%

Hệ thống Examon thiết kế hỗ trợ người học với 3 tiêu chí sau:

1: Rèn luyện khả năng tự học: Tự học luôn là yếu tố quan trọng quyết định

2: Học kỹ năng tư duy giải bài: Hầu hết học sinh hiểu bài nhưng không cách nào diễn đạt cho bạn mình hiểu cái mình đang hiểu là do thiếu kỹ năng này

3: Học từ lỗi sai: Nên dành nhiều thời gian để khám phá lỗi sai của chính mình chính là phương pháp học nhanh nhất, học từ cái sai của mình và học từ cái sai của người khác là 1 kỹ năng rất cần thiết cho mọi sự phát triển.

Từ tiêu chí số 3 Học từ lỗi sai đội ngũ chuyên môn đã nghiên cứu cách học và phát triển thành công công nghệ AI Gia sư Toán Examon với tính năng vượt trội hỗ trợ người học trong quá trình làm bài tập trên hệ thống đề thi Examon, gia sư AI sẽ ghi lại tất cả các lỗi sai của bạn đưa về hệ thống trung tâm dữ liệu để phân tích nhằm phát hiện năng lực của từng học sinh từ đó đưa ra các đề xuất bài tập phù hợp với từng cá nhân nhằm giúp người học rút ngắn thời gian luyện tập những kiến thức bị hỏng hoặc yếu nhất của mình tiến đến cải thiện kỹ năng làm bài thi giúp nhanh cán mốc ĐIỂM SỐ mình mơ ước.