Đại số 11 Cấp số nhân
Có rất nhiều bạn học sinh còn nhầm lẫn giữa cấp số nhân và cấp số cộng. Vậy nên hãy cùng Examon tìm hiểu về cấp số nhân nhé!
Mục lục bài viết
Cấp số nhân là một phần kiến thức xuất hiện nhiều trong các đề thi toán THPT. Việc hiểu rõ và áp dụng đúng các công thức cấp số nhân là thử thách vô cùng lớn đối với các bạn học sinh lớp 11. Vì vậy, Examon ở đây để cùng bạn tìm hiểu rõ hơn và chinh phục các công thức về cấp số nhân giúp cho bạn có thể dễ dàng hơn trong việc giải bài tập liên quan

1. Cấp số nhân là gì ?
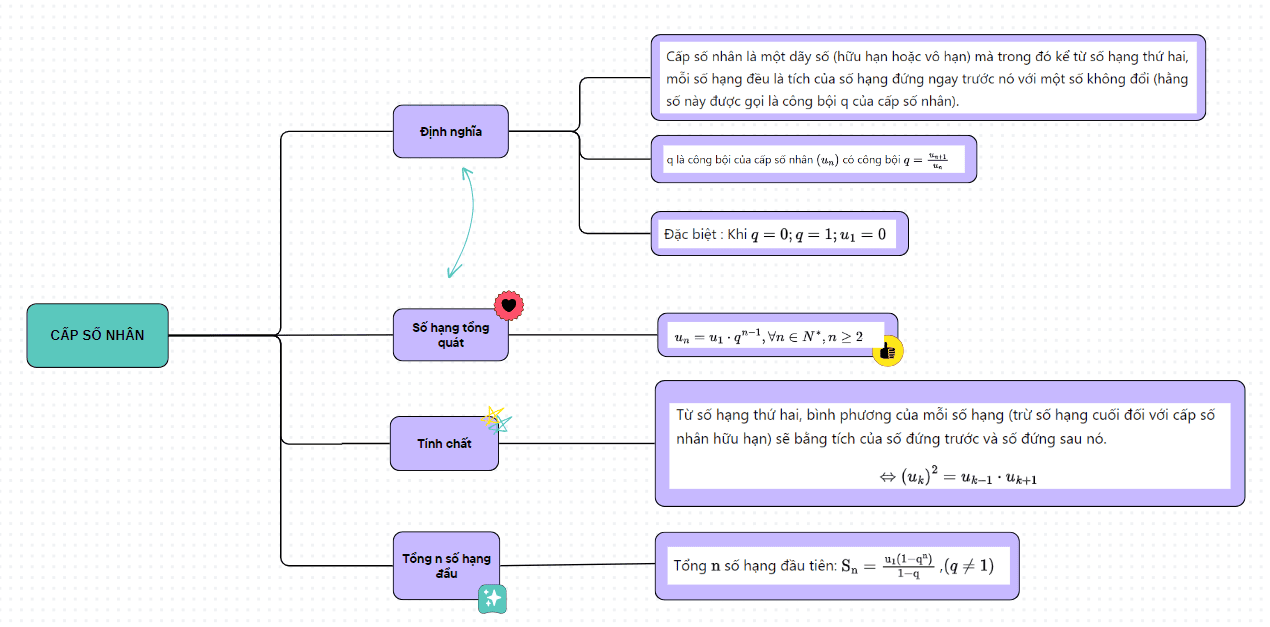
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn) mà trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi (hằng số này được gọi là công bội q của cấp số nhân).
Có nghĩa là: \(u_{n}\) là cấp số nhân với \(\Leftrightarrow \forall n \ge 2 , u_n=u_{n - 1}.q\) với \(n \in N^{\ast}\)
Như vậy, một cấp số nhân có dạng: \(\mathrm{u}_{\mathrm{n}}, \mathrm{u}_{\mathrm{n}} \mathrm{q}, \mathrm{u}_{\mathrm{n}} \mathrm{q}^{2}, \mathrm{u}_{\mathrm{n}} \mathrm{q}^{3} \ldots\)
Ví dụ: Dãy số \(\left(u_{n}\right)\), với \(u_{n}=2^{n}\) là một cấp số nhân với số hạng đầu \(u_{1}=2\) và công bội q = 2 .
2. Công bội q
q là công bội của cấp số nhân \(\left(u_{n}\right)\) có công bội \(q=\frac{u_{n+1}}{u_{n}}\)
Nếu \(\left(u_{n}\right)\) là cấp số nhân với công bội q, ta có công thức truy hồi: \(u_{n}=u_{n-1}\). q với \(n \in N^{*}\)
Ví dụ: Cho cấp số nhân \(u_{1}=2, u_{2}=6\). Tính công bội q
Ta có:
\[q=\frac{u_{2}}{u_{1}}=\frac{6}{2}=3\]Đặc biệt :
\(+q\gt 1\) \(\Rightarrow\) Cấp số nhân là dãy số tăng
\(+q=1\) \(\Rightarrow\) Cấp số nhân là dãy số không đổi có dạng \(\mathrm{u}_{1} ; \mathrm{u}_{1} ; \ldots \mathrm{u}_{1} ; \ldots\)
\(+0\lt q\lt 1\) \(\Rightarrow\) Cấp số nhân là dãy số giảm
\(+q=0\) \(\Rightarrow\) Cấp số nhân có dạng \(\mathrm{u}_{1} ; 0 ; 0 ; \ldots 0 ; \ldots\)
\(+q\lt 0\) \(\Rightarrow\) Cấp số nhân là dãy không tăng, không giảm
\(+\) Khi \(u_{1}=0\) thì với mọi q, cấp số nhân có dạng \(0 ; 0 ; 0 ; \ldots 0 ; \ldots\)
Ví dụ: Chứng minh rằng: dãy số hữu hạn sau là một cấp số nhân:
\(-4,1,-\frac{1}{4}, \frac{1}{16},-\frac{1}{64}\)
\[\begin{array}{l}1=\left(-\frac{1}{4}\right) \cdot(-4) \\\frac{1}{16}=\left(-\frac{1}{4}\right) \cdot\left(-\frac{1}{4}\right) \\-\frac{1}{4}=\left(-\frac{1}{4}\right) \cdot 1 \\-\frac{1}{16}=\left(-\frac{1}{4}\right) \cdot \frac{1}{16}\end{array}\]Vậy dãy số cho ở đề bài là cấp số nhân, \(q=-1 / 4\lt 0\) \(\Rightarrow\) Dãy số này là dãy số không tăng, không giảm.
3. Số hạng tổng quát của CSN
Số hạng tổng quát của cấp số nhân (un ) được xác định bởi công thức:
\[u_{n}=u_{1} \cdot q^{n-1} , \forall n \in N^{*}, n \geq 2\]Ví dụ: Cho cấp số nhân \(\left(u_{n}\right)\) thỏa mãn \(u_{1}=5, q=2\). Tính \(u_{5}\).
Ta có:
\[u_{5}=u_{1} q^{4}=5.2^{4}=80\]4. Tính chất các số hạng
\(\left(u_{n}\right)\) là một cấp số nhân thì từ số hạng thứ hai, bình phương của mỗi số hạng (trừ số hạng cuối đối với cấp số nhân hữu hạn) sẽ bằng tích của số đứng trước và số đứng sau nó.
\[\Leftrightarrow\left(u_{k}\right)^{2}=u_{k-1} \cdot u_{k+1}\]với \(k \geq 2\)
Ví dụ: Cho bốn số \(x ; 5 ; 25 ; y\) theo thứ tự đó lập thành một CSN. Tìm \(x, y\).
Ta có:
\[\begin{array}{l}5^{2}=x .25 \Leftrightarrow x=1 \\25^{2}=5 y \Leftrightarrow y=125\end{array}\]Vậy \(x=1, y=125\).
5. Tổng n số hạng đầu của một CSN
Tổng \(\mathrm{n}\) số hạng đầu tiên: \(\mathrm{S}_{\mathrm{n}}=\frac{\mathrm{u}_{1}\left(1-\mathrm{q}^{\mathrm{n}}\right)}{1-\mathrm{q}}\) ,\((q \neq 1)\)
Ví dụ: Cho cấp số nhân \(\left(u_{n}\right)\) thỏa mãn \(u_{1}=5, q=3\). Tính \(S_{10}\)
Ta có:
\[\begin{aligned}S_{10} & =\frac{u_{1}\left(1-q^{10}\right)}{1-q} \\& =\frac{5 \cdot\left(1-3^{10}\right)}{1-3} \\& =\frac{5\left(3^{10}-1\right)}{2}\end{aligned}\]6. Tổng hợp công thức tính cấp số nhân cơ bản
6.1. Dạng 1: Nhận dạng cấp số nhân
Phương pháp :
Bước 1: Tính \(q=\frac{u_{n+1}}{u_{n}}, \forall n \geq 1\)
Bước 2: Kết luận:
+ Nếu q là số không đổi thì dãy \(\left(u_{n}\right)\) là CSN.
+ Nếu q thay đổi theo \(\mathrm{n}\) thì dãy \(\left(u_{n}\right)\) không là \(\operatorname{CSN}\).
Ví dụ: Bài cho cấp số nhân \(U_{n}\) thỏa mãn: \(u_{n}=3^{\frac{n}{2}+1}\). Dãy số \(U_{n}\) trên là cấp số nhân đúng hay sai?
Ta có: \(\frac{u_{n}+1}{u_{n}}=\frac{3^{\frac{n+1}{2}+1}}{3^{\frac{n}{2}+1}}=\sqrt{3}=\) const không phụ thuộc vào n.
Vậy dãy số \(\left(U_{n}\right)\) là một cấp số nhân với số hạng đầu \(u_{1}=3 \sqrt{3}\) và công bội là \(q=\sqrt{3}\)
6.2. Dạng 2: Tìm q của cấp số nhân khi biết dạng tổng quát của dãy số cho trước
Phương pháp :
+ Xác định số hạng thứ nhất \(\mathrm{u}_{1}\) và số hạng thứ hai \(\mathrm{u}_{2}\) của dãy số
+ Áp dụng công thức: \(\mathrm{u}_{2}=\mathrm{u}_{1}\). \(\mathrm{q}\) từ đó suy ra: \(\mathrm{q}=\frac{u_{2}}{u_{1}}\)
Ví dụ: Biết dãy số \(\left(u_{n}\right)\) với \(u_{n}=(-3)^{n}\) là một cấp số nhân. Tìm công bội q của cấp số nhân đã cho?
Ta có: \(\mathrm{u}_{1}=(-3)^{1}=-3 ; \mathrm{u}_{2}=(-3)^{2}=9\)
Áp dụng công thức: \(\mathrm{u}_{2}=\mathrm{u}_{1} \cdot \mathrm{q}\)
Suy ra: \(q=\frac{u_{2}}{u_{1}}=\frac{9}{-3}=-3\)
Vậy, công bội của cấp số nhân là \(q=-3\)
6.3. Dạng 3: Tìm q của cấp số nhân khi biết lần lượt các số hạng trong dãy số
Phương pháp :
+ Đề bài cho trực tiếp dãy số \(\mathrm{u}_{1}, \mathrm{u}_{2}, \mathrm{u}_{3}, \ldots\). là một cấp số nhân.
+ Để tìm công bội q ta áp dụng công thức: \(q=\frac{u_{2}}{u_{1}}\)
Ví dụ: Biết dãy số -8, 40, -200, 1000 là một cấp số nhân. Tìm công bội q của cấp số nhân đã cho
Theo đề bài: \(\mathrm{u}_{1}=-8 ; \mathrm{u}_{2}=40\)
Công bội của cấp số nhân đã cho là:
\[q=\frac{u_{2}}{u_{1}}=\frac{40}{-8}=-5\]6.4. Dạng 4: Tìm q của cấp số nhân đựa theo định lí về số hạng tổng quát
Phương pháp :
Nếu một cấp số nhân có số hạng đầu \(\mathrm{u}_{1}\) và công bội \(\mathrm{q} \neq 0\) thì số hạng tổng quát \(\mathrm{u}_{\mathrm{n}}\) của nó được xác định bởi công thức: \(\mathrm{u}_{\mathrm{n}}=\mathrm{u}_{1}\). \(q^{n-1}\)
Ví dụ: Cho cấp số nhân \(\left(u_{n}\right)\) có công bội \(q\gt 0\). Biết \(u_{5}=9\) và \(u_{7}=36\). Tìm công bội \(q\) của cấp số nhân.
Ta có: \(u_{5}=u_{1} \cdot q^{4} ; u_{7}=u_{1} \cdot q^{6}\)
Lập tỉ số:\(\frac{u_{7}}{u_{5}}=\frac{u_{1} \cdot q^{6}}{u_{1} \cdot q^{4}}=q^{2}\)Mà \(\frac{u_{7}}{u_{5}}=\frac{36}{9}=4\)
Suy ra: \(q^{2}=4\).
Do đó, \(q=2\) (vì theo đề bài \(q>0\) )
Vậy, công bội của cấp số nhân là q = 2
6.5. Dạng 5: Xác định số hạng cấp số nhân
Phương pháp :
Để tìm số hạng của cấp số nhân ta sử dụng công thức tính số hạng tổng quát \(U_{n}=U_{1} \cdot q_{n-1}, n \geq 2\).
Ví dụ: Tìm \(u_{1}\) và q của cấp số nhân biết:
\[\left\{\begin{array}{c}u_{4}-u_{2}=72 \\u_{5}-u_{3}=144\end{array}\right.\]Ta biến đổi:
\[\begin{array}{l}\left\{\begin{array} { c } { u _ { 1 } q ^ { 3 } - u _ { 1 } q = 7 2 } \\{ u _ { 1 } q ^ { 4 } - u _ { 1 } q ^ { 2 } = 1 4 4 }\end{array} \Leftrightarrow \left\{\begin{array}{c}u_{1} q\left(q^{2}-1\right)=72 \\u_{1} q^{2}\left(q^{2}-1\right)=144\end{array}\right.\right. \\\Rightarrow q=\frac{144}{72}=2 \Rightarrow u_{1}=12\end{array}\]Vậy cấp số nhân \(\left(u_{n}\right)\) có \(u_{1}=12\) và \(q=2\)
6.6. Dạng 6: Tính tổng cấp số nhân của n số hạng đầu tiên trong dãy
Phương pháp :
Để tính tổng của CSN với n số hạng đầu tiên trong dãy số, ta sử dụng công thức:
\[S_{n}=u_{1}+u_{2}+\ldots+u_{n}=\frac{u_{1}\left(1-q^{n}\right)}{1-q}\]Ví dụ 1: Tính tổng cấp số nhân:
\[S=2+6+18+...+ 13122\]\(\left(u_{n}\right)\) có \(u_{1}=2\) và \(q=3\).
\[13122=u_{n}=u_{n} q^{n-1}=2.3^{n-1} \Leftrightarrow n=9 \Rightarrow S=S_{9}=u_{1} \frac{q_{0}-1}{q-1}\]Ví dụ 2: Cho cấp số cộng
\[\left(u_{n}\right):\left\{\begin{array}{c}u_{2}-u_{3}+u_{5}=10 \\u_{4}+u_{6}=26\end{array}\right.\]Hãy tính \(S=u_{1}+u_{4}+u_{7}+\ldots+u_{2011}\) ?
Ta có các số hạng \(u_{1}, u_{4}, u_{7}, \ldots, u_{2011}\) lập được thành một cấp số cộng bao gồm 670 số hạng và có công sai \( d' = 3 d \).
Do đó ta có:
\[S=\frac{670}{2}\left(2 u_{1}+669 d^{\prime}\right)=673015\]6.7. Dạng 7: Tìm cấp số nhân
Phương pháp :
+ Tìm các yếu tố xác định một CSN như: số hạng đầu \(u_{1}\), công bội \(q\).
+ Tìm công thức cho số hạng tổng quát \(u_{n} = u_{1} \cdot q^{n - 1} , n \ge 2\).
Ví dụ 1: Cho cấp số nhân \(\left(u_{n}\right)\) có các số hạng khác không, tìm \(u_{1}\) biết:
\[\left\{\begin{array}{c}u_{1}{ }^{2}+u_{2}^{2}+u_{3}{ }^{2}+u_{4}{ }^{2}=85 \\u_{1}+u_{2}+u_{3}+u_{4}=15\end{array}\right.\]Ta có:
\[\begin{array}{l}\left\{\begin{array} { l } { u _ { 1 } { } ^ { 2 } ( 1 + q ^ { 2 } + q ^ { 4 } + q ^ { 6 } ) = 8 5 } \\{ u _ { 1 } ( 1 + q + q ^ { 2 } + q ^ { 3 } ) = 1 5 }\end{array} \Leftrightarrow \left\{\begin{array}{l}u_{1} \frac{q^{4}-1}{q-1}=15 \\u_{1}{ }^{2} \frac{q^{8}-1}{q^{2}-1}=85\end{array}\right.\right. \\\Rightarrow\left(\frac{q^{4}-1}{q-1}\right)^{2}\left(\frac{q^{8}-1}{q^{2}-1}\right)=\frac{45}{17} \Leftrightarrow \frac{\left(q^{4}-1\right)(q+1)}{(q-1)\left(q^{4}+1\right)}=\frac{45}{17} \Leftrightarrow\left[\begin{array}{l}q=2 \\q=\frac{1}{2}\end{array}\right.\end{array}\]Từ đó ta tìm được \(\mathrm{u}_{1}=1, \mathrm{u}_{1}=8\).
Ví dụ 2: Cho \(\operatorname{CSN}\left(u_{n}\right)\) với \(u_{1}=-1 ; q=\frac{-1}{10}\). Số \(\frac{1}{10^{103}}\) là số hạng thứ mấy của \(\left(u_{n}\right)\) ?
\[\begin{array}{l}u_{n}=u_{1} \cdot q^{n-1} \Rightarrow \frac{1}{10^{103}}=-1 \cdot\left(-\frac{1}{10}\right)^{n-1} \\\Rightarrow n-1=103 \Rightarrow n=104\end{array}\]7. Ứng dụng trong thực tế
Cấp số nhân không chỉ là một khái niệm ở trong toán học mà còn có nhiều ứng dụng quan trọng trong đời sống và khoa học. Dưới đây là một số ứng dụng thực tế tiêu biểu:
+ Kinh tế và tài chính: CSN được sử dụng để tính toán lãi suất kép, một công cụ cơ bản trong đầu tư và tài chính. Ví dụ, giá trị tương lai của khoản đầu tư có thể được tính bằng cách áp dụng công thức của cấp số nhân với công bội là ( 1 + lãi suất).
+ Khoa học dân số: Trong dân số học, CSN giúp mô hình hóa sự tăng trưởng của dân số theo tỷ lệ phần trăm nhất định hàng năm. Ví dụ, nếu dân số của một khu vực tăng \(2 \%\) mỗi năm, cấp số nhân cho phép dự đoán dân số trong tương lai.
+ Vật lý và kỹ thuật: CSN cũng được sử dụng để tính toán sự giảm dần của các quá trình vật lý như phóng xạ hay giảm áp lực trong một môi trường thay đổi theo quy luật nhất định.
+ Thống kê và xác suất: Trong thống kê, các mô hình phân phối như phân phối hình chuông thường được mô tả thông qua các công thức có cấu trúc cấp số nhân.
+ Khoa học máy tính: Trong khoa học máy tính, các thuật toán như tìm kiếm nhị phân hoặc sắp xếp nhanh (quick sort) có thời gian chạy ứng với cấp số nhân, phản ánh độ phức tạp của chúng qua các bước lặp lại.
Cấp số nhân còn xuất hiện trong các bài toán thực tế khác như trong vận động mạo hiểm, ví dụ người nhảy bungee sẽ trải nghiệm sự giảm dần của độ cao sau mỗi lần bật lên, mô hình này có thể được mô tả bằng cấp số nhân.
Ví dụ: Một loại vi khuẩn được nuôi cấy trong phòng thí nghiệm, cứ mỗi phút số lượng lại tăng lên gấp đôi số lượng đang có. Từ một vi khuẩn ban đầu, hãy tính tổng số vi khuẩn có trong ống nghiệm sau 20 phút.
Tổng số vi khuẩn có trong ống nghiệm sau 20 phút là:
\[S_{20}=\frac{20 \cdot\left[1-2^{20}\right]}{1-2}=20971500\]8. Sơ đồ tư duy
9. Lời khuyên - Để học tốt cấp số nhân bạn cần những gì ?
Nắm chắc công thức và định nghĩa về cấp số nhân
Để có thể học tốt về cấp số nhân thì các em cần hiểu rõ về định nghĩa, tính chất và các công thức trong cách tính cấp số nhân.Việc nắm rõ định nghĩa và công thức cần phải hiểu về bản chất chứ không dừng lại ở việc học thuộc, học vẹt một cách máy móc.
Thay vào đó, các em nên đọc hiểu và phân tích chi tiết từng định nghĩa, tính chất kết hợp với việc làm bài tập để tạo ra phản xạ khi gặp các dạng bài quen thuộc.
Giải các bài tập từ cơ bản đến nâng cao
Nếu chỉ dừng lại ở việc hiểu thôi là chưa đủ mỗi em học sinh cần dành thời gian áp dụng những công thức vào các bài tập thực tế. Chính vì thế việc luyện tập các bài tập là một cách để các em có thể ghi nhớ các công thức nhanh nhất và các em có thể tìm tòi ra các cách giải mới, tiết kiệm thời gian hơn.
Luôn note lại những lỗi sai mà mình hay mắc phải
Ngoài học tập từ bạn bè, thầy cô việc mình tự rút ra kinh nghiệm từ những lỗi sai là phương pháp học nhớ lâu nhất và hiệu quả nhất.
Đặc biệt, các em học sinh không nên quá lệ thuộc vào thầy cô hay lời giải có sẵn. Trong quá trình học tập, có những lúc em làm sai hoặc không biết phương pháp giải thì chính những lúc đó giúp em tìm ra được những lỗ hổng kiến thức.
Thực hành những định nghĩa, công thức, tính chất vào làm các bài tập, đề thi
Việc làm nhiều bài tập giúp em vượt qua chuyên đề này một cách dễ dàng. Vì vậy, hãy sắp xếp thời gian làm các bài tập trong sách giao khoa, sách bài tập cũng đã giúp em nắm được kỹ năng để giải bài tập cấp số nhân.
10. Cách học hiệu quả
Chúng ta đã cùng nhau tìm hiểu về các định nghĩa, tính chất và công thức liên quan đến cấp số nhân. Đây là kiến thức cơ bản nhưng rất quan trọng trong việc giải các bài toán. Hy vọng rằng qua bài viết này đã giúp các bạn nắm vững và hiểu sâu hơn về cấp số nhân.
Việc ôn tập và luyện tập thường xuyên sẽ giúp các bạn nâng cao kiến thức và kỹ năng giải toán, từ đó đạt được kết quả cao trong kỳ thi THPT Quốc gia sắp tới. Hãy cùng Examon học tập và ôn tập nhé! Bạn có thể tham khảo phương pháp học tập hiệu quả của Examon.
Đã bao giờ bạn tự hỏi tại sao việc luyện đề lại quan trọng đến vậy không? Rất nhiều bạn đã mắc sai lầm nghiêm trọng khi luyện đề: Không phải mọi bộ đề đều giống nhau.
Nhiều bạn vẫn thường tìm kiếm và làm những bộ đề cũ kỹ, lỗi thời trên mạng mà không biết rằng chúng có thể không phản ánh chính xác chương trình học hay xu hướng ra đề mới nhất. Điều này không chỉ khiến bạn mất thời gian mà còn có thể dẫn đến những hiểu lầm về năng lực thực sự của mình.
Luyện đề đúng cách là phương pháp để bạn có thể nhận diện các dạng bài tập thường gặp, nắm vững phương pháp giải quyết hiệu quả và từ đó, nâng cao kỹ năng giải đề của mình. Với hệ thống đề được cập nhật liên tục và chính xác, Examon sẽ giúp bạn:
- Nhận diện các dạng bài thi quan trọng.
- Luyện tập với các phương pháp làm bài tối ưu.
- Thành thạo kỹ năng giải đề, sẵn sàng cho mọi kỳ thi.
Dưới đây, Examon sẽ hướng dẫn bạn cách luyện đề hiệu quả với hệ thống đề của Examon:
- Bước 1: Tạo và Đăng nhập tài khoản Đầu tiên, các bạn cần có một tài khoản Examon. Chỉ với vài thao tác đăng ký nhanh chóng, bạn đã sẵn sàng cho hành trình chinh phục kiến thức!
- Bước 2: Tiếp theo, hãy chọn lớp học, môn học mà bạn muốn luyện và khu vực bạn đang sống để Examon cung cấp đề thi phù hợp nhất với bạn.
- Bước 3: Lựa chọn đề thi và Bắt đầu luyện, Examon có hai chế độ: Luyện tập để bạn làm quen và Thi thử để kiểm tra năng lực. Hãy chọn một đề thi phù hợp và bắt đầu luyện!
- Bước 4: Khi làm bài, hãy tập trung và nghiêm túc như thể bạn đang ở trong phòng thi thật sự. Đây là cơ hội để rèn luyện sự tự tin và kỹ năng giải quyết vấn đề của bạn.
- Bước 5: Nhận điểm và Phân tích kết quả sau khi hoàn thành, bạn sẽ nhận được điểm số ngay lập tức cùng với lời giải chi tiết cho từng câu hỏi, giúp bạn hiểu rõ mình cần cải thiện ở đâu.
Tham khảo ngay bộ đề được biên soạn đặc biệt bám sát 99,9% đề tham khảo kỳ thi THPT năm 2024 của Examon ngay!
