Cách sử dụng Bảng Nguyên hàm hiệu quả trong giải Toán 12
Cùng Examon đi tìm hiểu và chinh phục kiến thức quý giá này nhé !
Mục lục bài viết
Bảng nguyên hàm - một bước tiến quan trọng trong thế giới toán học, một công cụ mạnh mẽ đối với việc giải quyết các bài toán thực tế và cơ sở cho việc hiểu sâu hơn về giải tích. Nhưng đây cũng là bước đầu khó khăn trong việc giải toán của bạn học sinh lớp 12, sự thách thức trong muôn vàn bài tập từ dễ đến khó.
Hiểu được điều này Examon sẽ cung cấp cho bạn nguồn thông tin kiến thức trọng tâm vô cùng quý giá về nguyên hàm mà đội ngũ chúng tôi đã chắt lọc được. Hãy bật chế độ học tập lên và cùng Examon đi tìm hiểu và chinh phục kiến thức quý giá này nhé !

1. Nhập môn nguyên hàm
1.1. Khái niệm
- Cho hàm số \(f(x)\) xác định trên khoảng \(K\). Hàm số \(F(x)\) được gọi là nguyên hàm của hàm số \(f(x)\)
Nếu: \(F^{\prime}(x)=f(x)\) với mọi \(x \in K\).
- Nhận xét:
Nếu \(F(x)\) là một nguyên hàm của \(f(x)\) thì \(F(x)+C,(C \in \mathbb{R})\) cũng là nguyên hàm của \(f(x)\).
- Ký hiệu: \(\int f(x) \mathrm{d} x=F(x)+C\).
1.2. Tích phân bất định
Tích phân bất định của hàm số \(f(x)\)
ký hiệu \(\int f(x) d x\), là tập hợp tất cả các nguyên hàm của hàm \(f(x)\).
Trong ký hiệu đó ta có:
- ký hiệu \(\int\) để chỉ tích phân bất định
- \(f(x) d x\) : gọi là biểu thức dưới dấu tích phân
- \(f(x)\) : gọi là hàm dưới dấu tích phân
- \(x\) : gọi là biến của tích phân.Để diễn tả rõ hơn khái niệm tích phân bất định ở trên, ta ký hiệu:
\[\int f(x) d x=F(x)+C .\]Trong đó \(F(x)\) là môt nguyên hàm của \(f(x), C\) là hằng số bất kỳ.
2. Bảng nguyên hàm
2.1. Sử dụng bảng nguyên hàm
1. \(\int 0 d x=C\)
2. \(\int d x=x+C\)
3. \(\int x^{\alpha} d x=\frac{1}{\alpha+1} x^{\alpha+1}+C(\alpha \neq-1)\)
4. \(\int \frac{1}{x^{2}} d x=-\frac{1}{x}+C\)
5. \(\int \frac{1}{x} d x=\ln |x|+C\)
6. \(\int c^{x} d x=c^{z}+C\)
7. \(\int a^{z} d x=\frac{a^{z}}{\ln a}+C\)
8. \(\int \cos x d x=\sin x+C\)
9. \(\int \sin x d x=-\cos x+C\)
10. \(\int \tan x \cdot d x=-\ln |\cos x|+C\)
11. \(\int \cot x \cdot d x=\ln |\sin x|+C\)
12. \(\int \frac{1}{\cos ^{2} x} d x=\tan x+C\)
13. \(\int \frac{1}{\sin ^{2} x} d x=-\cot x+C\)
14. \(\int\left(1+\tan ^{2} x\right) d x=\tan x+C\)
15. \(\int\left(1+\cot ^{2} x\right) d x=-\cot x+C\)
16. \(\int(a x+b)^{\alpha} \mathrm{dx}=\frac{1}{a} \frac{(a x+b)^{\alpha+1}}{\alpha+1}+c, \alpha \neq-1\)
17. \(\int x d x=\frac{x^{2}}{2}+C\)
18. \(\int \frac{\mathrm{dx}}{a x+b}=\frac{1}{a} \ln |a x+b|+c\)
19. \(\int c^{a s+b} d x=\frac{1}{a} c^{a s+b}+C\)
20. \(\int a^{k r+b} d x=\frac{1}{k} \frac{a^{k+b}}{\ln a}+C\)
2.2. Bài tập
Bài 1:
\(I=\int \frac{1}{x^{4}} d x=\int x^{-4} d x\)
\(=\frac{x^{-3}}{-3}+C=-\frac{1}{3 x^{3}}+C\).
Bài 2:
\(I=\int \frac{1}{x^{2}\left(1+x^{2}\right)} d x=\int\left(\frac{1}{x^{2}}-\frac{1}{1+x^{2}}\right) d x\)
\(=-\frac{1}{x}-a c r \tan x+C\)
Bài 3:
\(I=\int e^{x}\left(2^{x}+\frac{e^{-x}}{\sqrt{1-x^{2}}}\right) d x\)
\(=\int(2 e)^{x} d x+\int \frac{d x}{\sqrt{1-x^{2}}}\)
\(=\frac{(2 e)^{x}}{\ln 2 e}+a c r \sin x+C\)
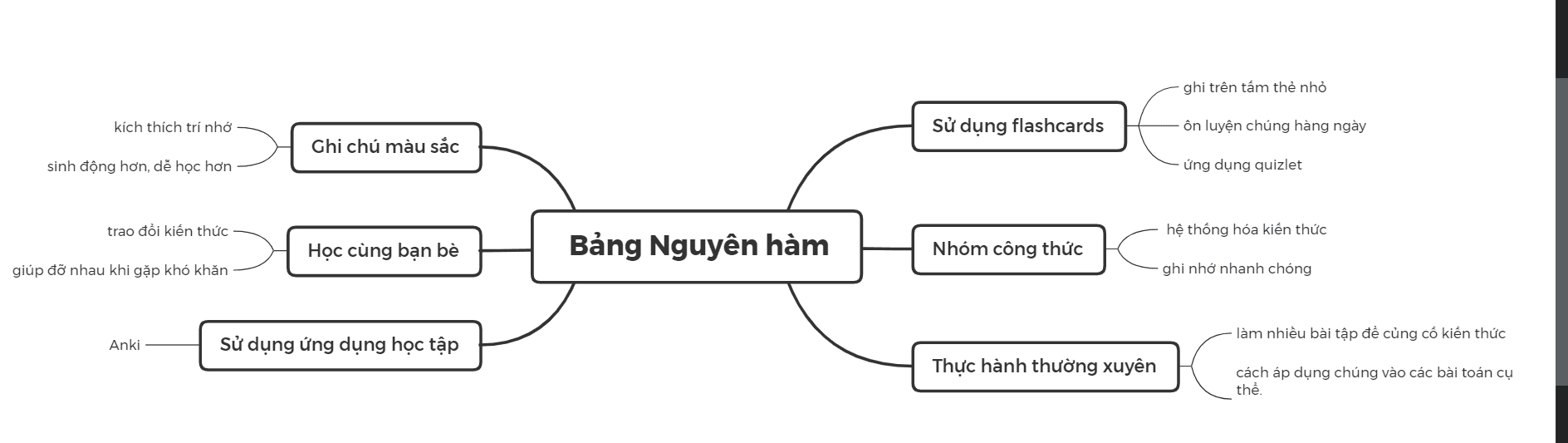
3. Mẹo hay học bảng nguyên hàm
Nguyên hàm không chỉ đơn thuần là việc ghi nhớ các công thức mà còn đòi hỏi sự hiểu biết sâu rộng vể cách chúng được áp dụng trong các bài toán khác nhau. Với sự đa dạng và phức tạp của các công thức nguyên hàm, Bảng Nguyên hàm đôi khi bạn có thể cảm thấy choáng ngợp và mất phương hướng.
Tuy nhiên, học tập không phải lúc nào cũng là một hành trình gian nan nếu chúng ta biết cách tiếp cận một cách thông minh và hiệu quả. Để giúp bạn vượt qua khó khăn này, chúng tôi đã tổng hợp một số mẹo học tập hiệu quả, giúp bạn không chỉ ghi nhớ bảng nguyên hàm một cách dễ dàng mà còn thực sự hiểu và áp dụng chúng một cách linh hoạt.
Dưới đây là những lời khuyên và mẹo hay mà bạn có thể áp dụng ngay hôm nay để cải thiện việc học bảng nguyên hàm của mình.
4. Giải pháp cho việc luyện đề hiệu quả
Đã bao giờ bạn tự hỏi tại sao việc luyện đề lại quan trọng đến vậy không?
Rất nhiều bạn đã mắc sai lầm nghiêm trọng khi luyện đề: Không phải mọi bộ đề đều giống nhau.
Nhiều bạn vẫn thường tìm kiếm và làm những bộ đề cũ kỹ, lỗi thời trên mạng mà không biết rằng chúng có thể không phản ánh chính xác chương trình học hay xu hướng ra đề mới nhất. Điều này không chỉ khiến bạn mất thời gian mà còn có thể dẫn đến những hiểu lầm về năng lực thực sự của mình.

Luyện đề đúng cách là phương pháp để bạn có thể nhận diện các dạng bài tập thường gặp, nắm vững phương pháp giải quyết hiệu quả và từ đó, nâng cao kỹ năng giải đề của mình.
Với hệ thống đề được cập nhật liên tục và chính xác, Examon sẽ giúp bạn:
- Nhận diện các dạng bài thi quan trọng.
- Luyện tập với các phương pháp làm bài tối ưu.
- Thành thạo kỹ năng giải đề, sã̃n sàng cho mọi kỳ thi.
Dưới đây, Examon sẽ hướng dẫn bạn cách luyện đề hiệu quả với hệ thống đề của Examon:
- Bước 1: Tạo và Đăng nhập tài khoản Đầu tiên, các bạn cần có một tài khoản Examon. Chỉ với vài thao tác đăng ký nhanh chóng, bạn đã sã̃n sàng cho hành trình chinh phục kiến thức!
- Bước 2: Tiếp theo, hãy chọn lớp học, môn học mà bạn muốn luyện và khu vực bạn đang sống để Examon cung cấp đề thi phù hợp nhất với bạn.
- Bước 3: Lựa chọn đề thi và Bắt đầu luyện, Examon có hai chế độ: Luyện tập để bạn làm quen và Thi thử để kiểm tra năng lực. Hãy chọn một đề thi phù hợp và bắt đầu luyện!
- Bước 4: Khi làm bài, hãy tập trung và nghiêm túc như thể bạn đang ở trong phòng thi thật sự. Đây là cơ hội để rèn luyện sự tự tin và kỹ năng giải quyết vấn đề của bạn.
- Bước 5: Nhận điểm và Phân tích kết quả sau khi hoàn thành, bạn sẽ nhận được điểm số ngay lập tức cùng với lời giải chi tiết cho từng câu hỏi, giúp bạn hiểu rõ mình cần cải thiện ở đâu.
Tham khảo ngay bộ đề được biên soạn đặc biệt bám sát \(99.9 \%\) đề tham khảo kỳ thi THPT năm 2024 của Examon ngay!