Cho hình chóp \(S . A B C D\) có \(S A \perp(A B C D)\) và đáy \(A B C D\) là hình vuông cạnh \(a\). Khoảng cách từ \(C\) đến \((S A D)\) bằng
A.
\(2 a\).
B.
\(a\)
C.
\(a \sqrt{3}\).
D.
\(\frac{a}{2}\).
Giải thích:
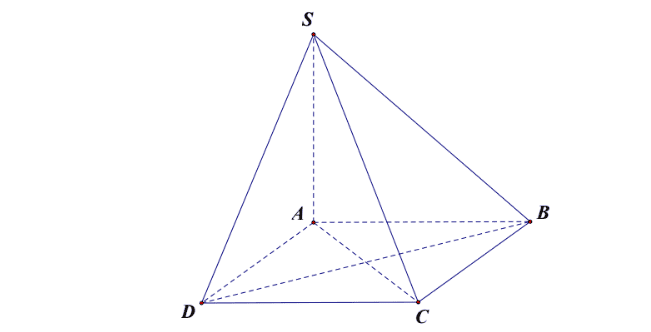
Ta có \(\left.\begin{array}{l}C D \perp S A \\ C D \perp A D\end{array}\right\} \Rightarrow C D \perp(S A D)\)
Do đó \(\Rightarrow d(C,(S A D))=C D=a\)
Câu hỏi này nằm trong: