Cho hàm số \(f(x)\) có bảng biến thiên của hàm số \(f^{\prime}(x)\) như sau:Số điểm cực trị của hàm số \(y=f\left(1-x^{2}\right)\) là:
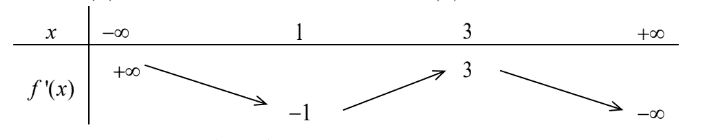
A.
2 .
B.
3 .
C.
4 .
D.
5 .
Giải thích:
Ta có \(y^{\prime}=\left[f\left(1-x^{2}\right)\right]=-2 x f^{\prime}\left(1-x^{2}\right)\)
\(\begin{array}{l}y^{\prime}=0 \Leftrightarrow\left[\begin{array} { l } { x = 0 } \\{ f ^ { \prime } ( 1 - x ^ { 2 } ) = 0 }\end{array} \Leftrightarrow \left[\begin{array} { l } { x = 0 } \\{ 1 - x ^ { 2 } = a \in ( - \infty ; 1 ) } \\{ 1 - x ^ { 2 } = b \in ( 1 ; 3 ) } \\{ 1 - x ^ { 2 } = c \in ( 3 ; + \infty ) }\end{array} \Leftrightarrow \left[\begin{array}{l}x=0 \\x^{2}=1-a \in(0 ;+\infty) \\x^{2}=1-b \in(-2 ; 0)(v n) \\x^{2}=1-c \in(-\infty ;-2) \text { (vn) }\end{array}\right.\right.\right. \\\Leftrightarrow\left[\begin{array}{l}x=0 \\x= \pm \sqrt{1-a} \neq 0\end{array} \text { là } 3\right. \text { nghiệm đơn phân biệt }\end{array}\)Vậy hàm số \(y=f\left(1-x^{2}\right)\) có 3 diĉ̉m cực trị.
Câu hỏi này nằm trong: