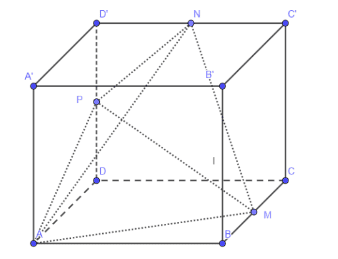
Cho hình hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có \(M, N, P\) lần lượt là trung điểm các cạnh \(B C, C^{\prime} D^{\prime}, D D^{\prime}\) (tham khảo hình vẽ). Biết thể tích khối hộp bằng 144 , thể tích khối tứ diĉ̣n \(A M N P\) bằng
A.
15 .
B.
24 .
C.
20 .
D.
18 .
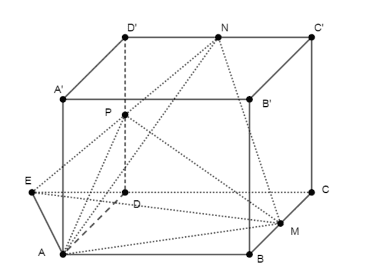
Giải thích:
Câu hỏi này nằm trong: