Cho hàm số \(y=-x^{2}+2 x-5\). Khi đó:
d) Giá trị lớn nhất của hàm số là \(y_{\max }=-4\), khi \(x=2\)
A.
True
B.
False
Giải thích:
\[y=-x^{2}+2 x-5 ;(a=-1, b=2, c=-5) .\]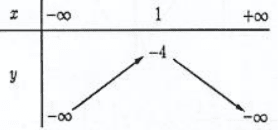
Tập xác định: \(D=\mathbb{R}\). Tọa độ đỉnh \(I\) của parabol:
\[x_{I}=-\frac{b}{2 a}=1, y_{I}=-1^{2}+2.1-5=-4 \text { hay } I(1 ;-4)\]Định hướng cho bảng biến thiên: Do \(a=-1\lt 0\) nên bề lõm parabol hướng xuống.
Bảng biến thiên:

Kết luận:
Hàm số đã cho đồng biến trên khoảng \((-\infty ; 1)\) và nghịch biến trên khoảng
\[(1 ;+\infty)\]Giá trị lớn nhất của hàm số là \(y_{\max }=-4\), khi \(x=1\). (Hàm số không có giá trị nhỏ nhất)
Câu hỏi này nằm trong: