Cho hình chóp \(S . A B C\) có đáy \(A B C\) là tam giác vuông cân tại \(C\). Tam giác \(S A B\) vuông cân tại \(S\) và \(\widehat{B S C}=60^{\circ} ; S A=a\). Gọi \(M, N\) lần lượt là trung điểm cạnh \(S B, S A, \varphi\) là góc giữa đường thẳng \(A B\) và \(C M\).
a) Độ dài đoạn thẳng \(A B\) bằng \(a \sqrt{3}\)
A.
B.
Giải thích:
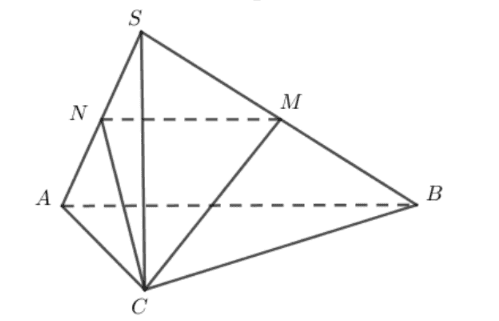
Đặt \(S A=a\).
Suy ra \(S B=C A=C B=a\) và \(A B=a \sqrt{2}\).
Lại có \(\widehat{B S C}=60^{\circ}\).
Suy ra tam giác \(S B C\) đều nên \(S C=a\).
Suy ra \(C M=C N=\frac{a \sqrt{3}}{2}\) hay \(M N\) song song với \(A B\).
Khi đó \(\widehat{(A B, C M)}=\widehat{(M N, C M)}\).
Áp dụng định lí cosin vào tam giác \(C M N\) \(\cos \widehat{\mathrm{CMN}}=\frac{M C^{2}+M N^{2}-C N^{2}}{2 M C \cdot M N}=\frac{\sqrt{6}}{6}\)
\(\Rightarrow \cos (A B, C M)=\cos (M N, C M)=|\cos \widehat{C M N}|=\frac{\sqrt{6}}{6}\).
Câu hỏi này nằm trong: