Cho hình chóp đều \(S . A B C D\) có đáy cạnh a và chiều cao \(S O=2 a\). Gọi \(M, N, P\) , \(Q\) lần lượt là trung điểm của \(S A, S B, S C, S D\). Tính thể tích khối chóp cụt đều ABCD.MNPQ.
Giải thích:
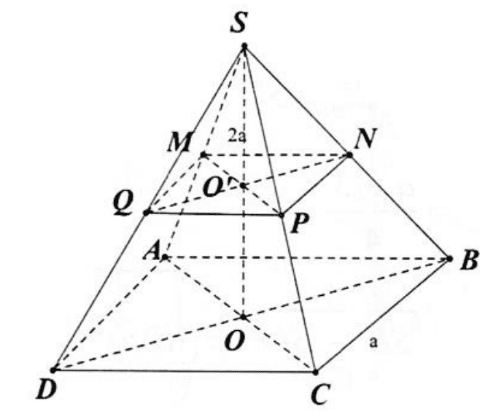
\(\begin{array}{l}V=\frac{1}{3}\left(S_{A B C D}+S_{M N P Q}+\sqrt{S_{A B C D} .S_{M N P Q}}\right). O O^{\prime} \\ S_{A B C D}=a^{2} \\ S_{M N P Q}=\left(\frac{1}{2} a\right)^{2}=\frac{1}{4} a^{2} \\ \Rightarrow V=\frac{1}{3}\left(a^{2}+\frac{1}{4} a^{2}+\sqrt{a^{2} .\frac{1}{4} a^{2}}\right) . a=\frac{7}{12} a^{3}\end{array}\)
Câu hỏi này nằm trong: