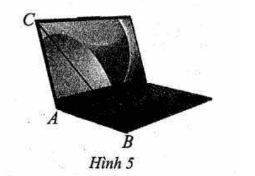
Hình ảnh máy tính xách tay ở Hình 5 gợi nên góc nhị diện và số đo góc \(B A C\) được gọi là độ mở của máy tính.
d) Độ mở máy tính là \(120^{\circ}\) nếu \(A B=A C=30 \mathrm{~cm}\) và \(B C=30 \sqrt{3}\).
A.
True
B.
False
Giải thích:
Ta có: \(\cos B A C=\frac{A B^{2}+A C^{2}-B C^{2}}{2 A B \cdot A C}\).
Nếu \(A B=A C=30 \mathrm{~cm}\) và \(B C=30 \sqrt{3} \mathrm{~cm}\) thì:
\(\cos B A C=\frac{30^{2}+30^{2}-30^{2} \cdot 3}{2 \cdot 30 \cdot 30}=-\frac{1}{2}\).
Suy ra \(B A C=120^{\circ}\), khi đó độ mở của máy tính là \(120^{\circ}\).
Câu hỏi này nằm trong: