Trước một tòa nhà, người ta làm một cái hồ bơi có dạng hình elip với độ dài hai bán trục lần lượt là \(3 m\) và 5 m . Xét hệ trục tọa độ \(O x y\) (đơn vị trên các trục là mét) có hai trục tọa độ chứa hai trục của elip, gốc tọa độ \(O\) là tâm của elip (hình)
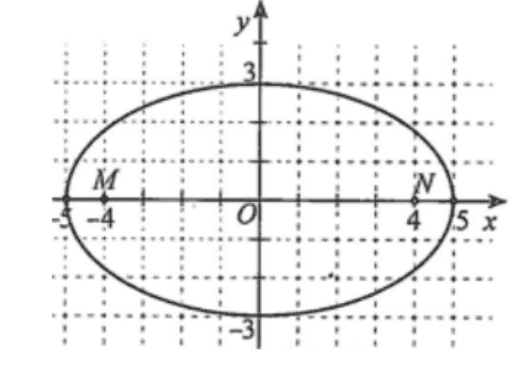
Xét các điểm \(M, N\) cùng thuộc trục lớn của elip và đều cách \(O\) một khoảng bằng \(4 m\) về hai phía của\(O\). Tổng khoảng cách từ mọi điểm trên đường elip đến \(M\) và \(N\) luôn bằng 10 m
A.
B.
Giải thích:
Ta có: \(a=5, b=3\) nên \(c^{2}=a^{2}-b^{2}=25-9=16\), suy ra \(c=4\).
Các tiêu điểm của elip có toạ độ là \((-4 ; 0)\) và \((4 ; 0)\).
Vậy \(M\) và \(N\) chính là các tiêu điểm của elip.
Vì vậy, tổng khoảng cách từ mọi điểm trên đường elip đến \(M\) và \(N\) luôn bằng \(2 a=10 m\) không đổi.
Câu hỏi này nằm trong: