Cho hình chóp tứ giác đều \(S . A B C D\) có cạnh đáy bằng \(a\), tâm \(O\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(S A\) và \(B C\). Gọi \(F\) là giao điểm của \(A N\) và \(C D\). Biết rằng góc giữa \(M N\) và \((A B C D)\) bằng \(60^{\circ}\).
b) Góc giữa \((M N,(A B C D))\) và \(=(S F,(A B C D))\) bằng nhau.
A.
B.
Giải thích:
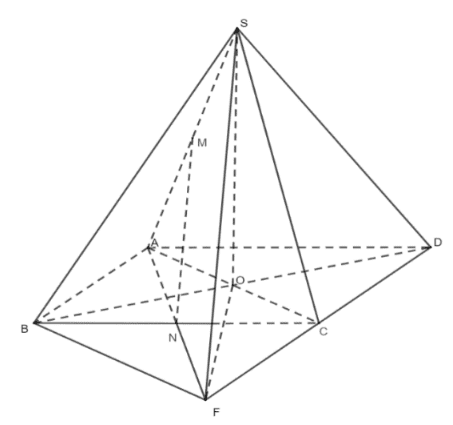
Ta có \(A N \cap C D=F\) (suy ra \(N\) là trung điểm của \(A F, N C\) là đường trung bình trong tam giác \(A F D) \Rightarrow M N / / S F ;(M N,(A B C D))=(S F,(A B C D))=\widehat {S F O}=60^{\circ}\).
Vó́i \(O C=\frac{1}{2} A C=\frac{1}{2} \sqrt{A B^{2}+B C^{2}}=\frac{a \sqrt{2}}{2} ; C F=C D=a\).
\[\Rightarrow O F=\sqrt{a^{2}+\frac{a^{2}}{2}-2 a \frac{a \sqrt{2}}{2} \cos 135^{\circ}}=\frac{a \sqrt{10}}{2} \Rightarrow S F=\frac{O F}{\cos 60^{\circ}}=\frac{a \sqrt{10}}{2}: \frac{1}{2}=a \sqrt{10} \text {. }\]Ta có \(O C \perp B D, O C \perp S O \Rightarrow O C \perp(S B D)\), lại có \(O C / / B F \Rightarrow B F \perp(S B D)\),
Do vậy \((M N,(S B D))=(S F,(S B D))=F S B\).
\(B F=2 O C=a \sqrt{2}(O C\) là đường trung bình trong tam giác \(B D F)\)
Suy ra \(S B=\sqrt{S F^{2}-B F^{2}}=2 \sqrt{2} a\).
Vậy \(\cos \widehat {B S F}=\frac{S B}{S F}=\frac{2 \sqrt{5}}{5}\).
Câu hỏi này nằm trong: