Cho hình vuông \(A B C D\) nội tiếp đường tròn \((O)\). Gọi \(M\) là một điểm bất kì trên cạnh \(B C(M\) khác \(B\) và \(C), N\) là điểm trên cạnh \(C D\) sao cho \(B M=C N\). Gọi \(H, I\) lần lượt là giao điểm của \(A M\) với \(B N, D C\).
a) Chứng minh tứ giác \(A H N D\) nội tiếp và \(M N\) vuông góc với \(B I\).
Giải thích:
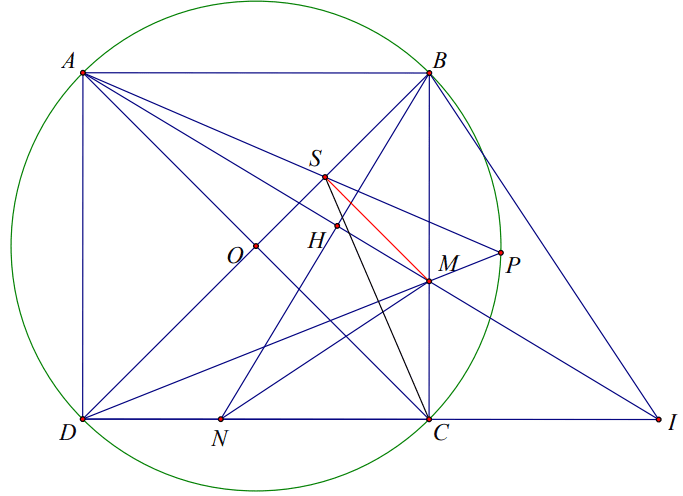
Ta có: \(\mathrm{BM}=\mathrm{CN}, \mathrm{AB}=\mathrm{BC}, \angle B=\angle C=90^{\circ}\)
Nên \(\triangle A B M=\triangle B C N\) (c.g.c)
Mà \(\angle B A M+\angle B M A=90^{\circ} \Rightarrow \angle C B N+\angle B M A=90^{\circ} \Rightarrow \angle B H M=90^{\circ}\)
Suy ra \(\angle A D N+\angle A H N=180^{\circ}\), hay tứ giác \(\mathrm{ADNH}\) nội tiếp \(\Rightarrow \mathrm{IH} \perp \mathrm{BN}\)
Ta có \(\mathrm{BC} \perp \mathrm{CD}(\mathrm{gt}) \Rightarrow \mathrm{BC} \perp \mathrm{NI}\)
Do đó \(\mathrm{M}\) là trực tâm của tam giác \(\mathrm{BIN}\) nên \(\mathrm{NM} \perp \mathrm{BI}\) (đpcm).
Câu hỏi này nằm trong: