Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có cạnh là \(a\gt 0\). Khi đó, khoảng cách giữa hai đường thẳng chéo nhau \(A B^{\prime}\) và \(B C^{\prime}\) là
A.
\(\frac{a \sqrt{3}}{2}\).
B.
\(\frac{a \sqrt{3}}{3}\).
C.
\(\frac{a \sqrt{2}}{3}\)
D.
\(\frac{a \sqrt{6}}{3}\).
Giải thích:
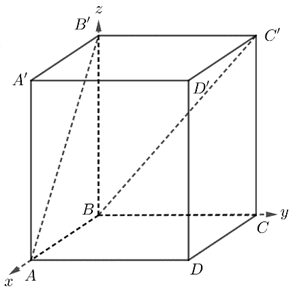
Gọi \(O\) là tâm hình vuông \(A B C D\).
Trong mặt phẳng \(\left(A C C^{\prime} A^{\prime}\right)\), kẻ \(C H \perp C^{\prime} O\) tại \(H\), mà \(C H \perp B D\) (do \(B D \perp\left(A C C^{\prime} A^{\prime}\right)\) ) nên \(C H \perp\left(C^{\prime} B D\right) \Rightarrow d\left(C ; C^{\prime} B D\right)=C H\)
Ta có: \(A B^{\prime} / /\left(C^{\prime} B D\right) \Rightarrow d\left(A B^{\prime}, B C^{\prime}\right)=d\left(A B^{\prime},\left(C^{\prime} B D\right)\right)=d\left(A,\left(C^{\prime} B D\right)\right)=d\left(C,\left(C^{\prime} B D\right)\right)=C H\)
Xét \(\Delta C^{\prime} C O\) vuông tại \(C\), đường cao \(C H\) :
\(\frac{1}{C H^{2}}=\frac{1}{C O^{2}}+\frac{1}{C C^{\prime 2}}=\frac{3}{a^{2}} \Rightarrow C H=\frac{a \sqrt{3}}{3} \text {. }\)Câu hỏi này nằm trong: