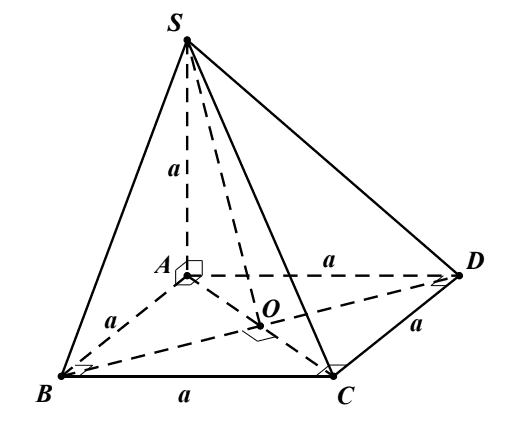
Ta có \(\left\{\begin{array}{l}B O \perp A C \\ B O \perp S A\end{array} \Rightarrow B O \perp(S A C)(1)\right.\) mà \(S B \cap(S A C)=S\) (2)
Từ (1) và \((2) \Rightarrow S O\) là hình chiếu của \(S B\) lên \((S A C)\).
Do đó \((S B,(S A C))=(S B, S O)\).
Ta có \(B O=\frac{B D}{2}=\frac{A B \sqrt{2}}{2}=\frac{a \sqrt{2}}{2}\).
Mặt khác \(S B=\sqrt{S A^{2}+A B^{2}}=a \sqrt{2}\).
Trong tam giác \(S O B\) vuông tại \(O\), ta có \(\sin B S O=\frac{B O}{S B}=\frac{1}{2} \Rightarrow B S O=30^{\circ}\).
Vậy \((S B,(S A C))=B S O=30^{\circ}\).