Cho tam thức bậc hai \(f(x)=x^{2}-\frac{1}{x}\). Các mệnh đề sau đúng hay sai?
a) Điều kiện: \(x \neq 0\).
A.
True
B.
False
Giải thích:
\(f(x)=x^{2}-\frac{1}{x}=\frac{x^{3}-1}{x}=\frac{(x-1)\left(x^{2}+x+1\right)}{x} .\)
Điều kiện: \(x \neq 0\).
Xét \(f(x)=0 \Rightarrow(x-1)\left(x^{2}+x+1\right)=0 \Rightarrow\left[\begin{array}{l}x=1 \\ x^{2}+x+1\end{array}\right.\) (vô nghiệm) \(\Rightarrow x=1\)
Bảng xét dấu \(f(x)\) :
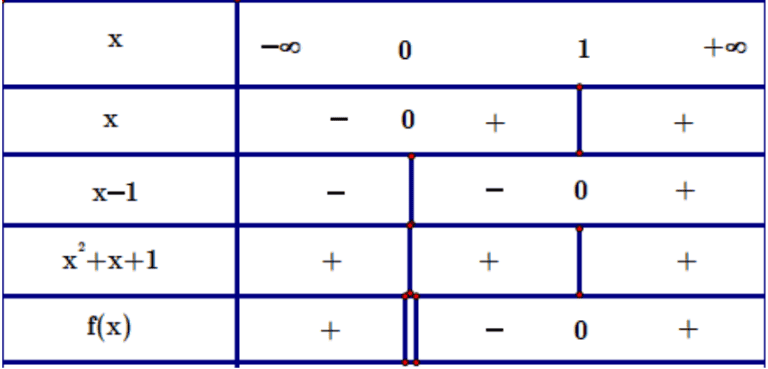
Kết luận: \(f(x)\gt 0, \forall x \in(-\infty ; 0) \cup(1 ;+\infty) ; f(x)\lt 0, \forall x \in(0 ; 1)\).
Câu hỏi này nằm trong: