Cho hình chóp \(\mathrm{S} . \mathrm{ABCD}\) có đáy là hình vuông cạnh bằng \(2 \sqrt{2}\), tam giác \(\mathrm{SAB}\) vuông cân tại \(\mathrm{S}\) và nằm trong mặt phẳng vuông góc với \((\mathrm{ABCD})\). Tính khoảng cách giữa hai đường thẳng \(\mathrm{BC}\) và \(\mathrm{SA}\).
Giải thích:
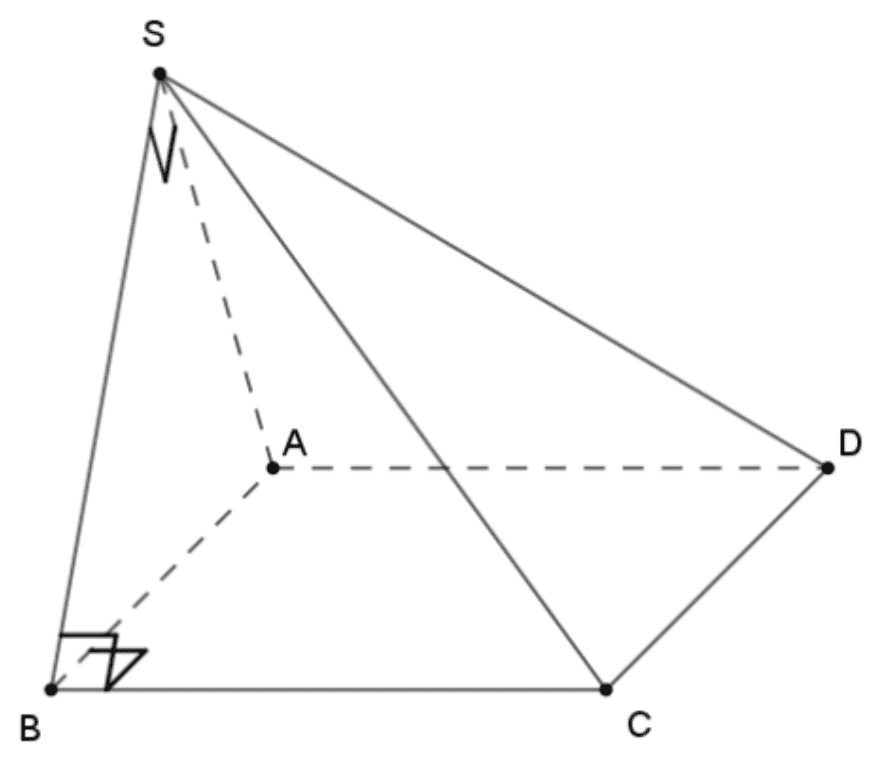
Ta có \(\left\{\begin{array}{l}(S A B) \cap(A B C D) \\ (S A B) \perp(A B C D) \Rightarrow B C \perp(S A B) \Rightarrow B C \perp S B \\ B C \perp A B\end{array}\right.\)
Tam giác \(S A B\) vuông cân tại \(S\) nên ta có \(S B \perp S A\)
Vậy \(S B\) là đường vuông góc chung của \(B C\) và \(S A\).
Suy ra \(d(S A, B C)=S B\)
Tam giác \(S A B\) vuông cân tại \(S\) và \(A B=2 \sqrt{2} \Rightarrow S B=2\)
Vậy \(d(S A, B C)=2\)
Câu hỏi này nằm trong: