Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình chữ nhật, \(A B=2 a, A D=a\). SA vuông góc với mặt phẳng đáy. \(S A=a \sqrt{3}\). Cosin của góc giữa \(S C\) và mặt đáy bằng:
A.
\(\frac{\sqrt{5}}{4}\).
B.
\(\frac{\sqrt{7}}{4}\).
C.
\(\frac{\sqrt{6}}{4}\).
D.
\(\frac{\sqrt{10}}{4}\).
Giải thích:
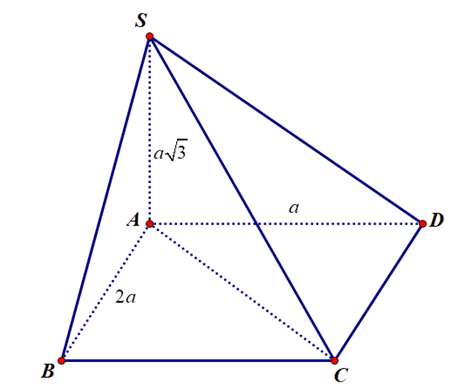
Hình chiếu của \(S C\) lên \((A B C D)\) là \(A C\)
Do đó \([\overline{S C,(A B C D)}]=\widetilde{S C A}\)
\(A C=\sqrt{A B^{2}+A D^{2}}=\sqrt{4 a^{2}+a^{2}}=a \sqrt{5} \Rightarrow S C=2 a \sqrt{2}\)Trong tam giác vuông SAC:\(\cos \widehat{S C A}=\frac{A C}{S C}=\frac{a \sqrt{5}}{2 a \sqrt{2}}=\frac{\sqrt{10}}{4}\).
Câu hỏi này nằm trong: