Cho tứ diện \(A B C D\). Gọi \(H\) là trực tâm của tam giác \(B C D\) và \(A H \perp(B C D)\). Khẳng định nào dưới đây đúng?
A.
\(C D \perp B D\)
B.
\(A B \perp C D\)
C.
\(A C=B D\)
D.
\(A B=C D\)
Giải thích:
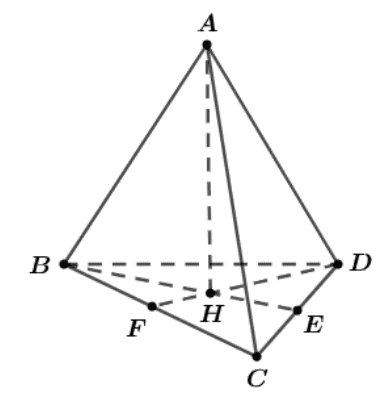
Do \(A H \perp(B C D) \Rightarrow A H \perp C D\). Tam giác \(B C D\) có 2 đường cao là \(B E, D F\).
Ta có: \(\left\{\begin{array}{l}C D \perp A H \\ C D \perp B E\end{array} \Rightarrow C D \perp(A B E) \Rightarrow C D \perp A B\right.\).
Câu hỏi này nằm trong: