Cho hình chóp \(S A B C\) có đáy \(A B C\) là tam giác vuông tại \(B, S A\) vuông góc với mặt phẳng \((A B C), A H\) là đường cao trong tam giác \(S A B\) Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
\(A H \perp A C\).
B.
\(A H \perp B C\).
C.
\(S A \perp B C\).
D.
\(A H \perp S C\)
Giải thích:
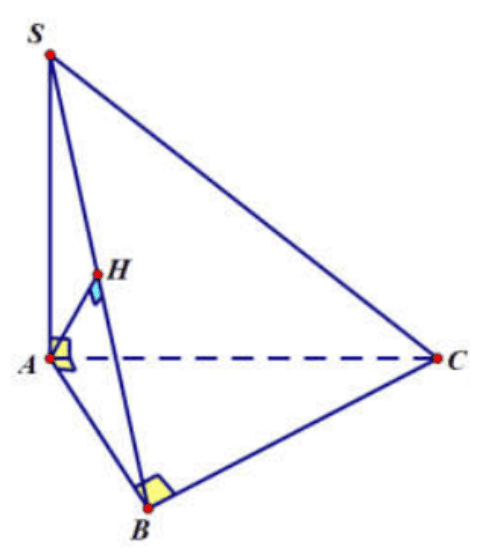
Do \(S A \perp(A B C) \Rightarrow S A \perp B C\) nên \(\mathbf{C}\) đúng.
Ta có: \(\left\{\begin{array}{l}B C \perp S A \\ B C \perp A B \quad(\mathrm{gt})\end{array} \Rightarrow B C \perp(S A B) \Rightarrow B C \perp A H\right.\) nên \(\mathbf{B}\) đúng.
Mà: \(S B \perp A H\)
Từ (1),(2) suy ra: \(A H \perp(S B C)\)
\(\Rightarrow A H \perp S C\) nên \(\mathbf{D}\) đúng.
Vậy A sai.
Câu hỏi này nằm trong: