Cho tam giác \(A B C\) đều cạnh \(3 a\). Lấy các điểm \(M, N\) lần lượt trên các cạnh \(B C, C A\) sao cho \(B M=a, C N=2 a\).
a) Tìm giá trị của tích vô hướng \(\overrightarrow{A M} \cdot \overrightarrow{B C}\) theo \(a\).
Giải thích:
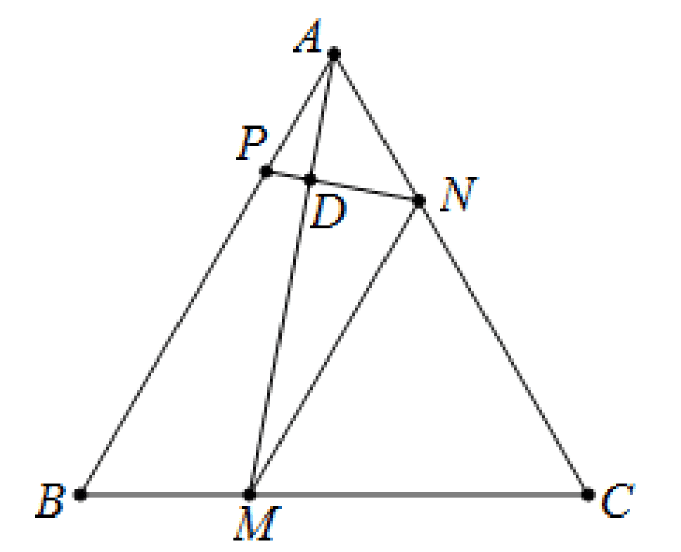
\(\begin{array}{l}\text {Ta có } \overrightarrow{A M} \cdot \overrightarrow{B C}=(\overrightarrow{A B}+\overrightarrow{B M}) \cdot \overrightarrow{B C}=\overrightarrow{A B} \cdot \overrightarrow{B C}+\overrightarrow{B M} \cdot \overrightarrow{B C} \\ =3 a \cdot 3 a \cdot \cos 120^{\circ}+a \cdot 3 a \cdot \cos 0^{\circ}=-\frac{9}{2} a^{2}+3 a^{2}=-\frac{3}{2} a^{2} .\end{array}\)
Câu hỏi này nằm trong: