Xét nửa đường tròn đường kính \(M N=10\). Xét điểm \(B\) (không trùng hai điểm \(M, N\) ) di động trên nửa đường tròn và hình chiếu của \(B\) trên đoạn \(M N\) là điểm \(A\), vẽ hình chữ nhật \(A B C D\) với \(C\) cũng thuộc nửa đường tròn. Tìm độ dài \(I A\) biết rằng chu vi hình chữ nhật \(A B C D\) bằng 22 .
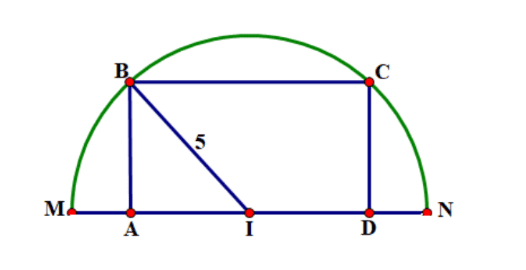
Giải thích:
Đặt \(I A=x \in(0 ; 5) \Rightarrow A D=2 x\).
Xét tam giác \(I A B\) vuông tại \(A\), ta có: \(A B=\sqrt{5^{2}-x^{2}}\).
Chu vi hình chữ nhật \(A B C D\) là:
\(\begin{array}{l}2 A B+2 A D=4 x+2 \sqrt{5^{2}-x^{2}}=22 \Leftrightarrow \sqrt{25-x^{2}}=11-2 x \\\Leftrightarrow\left\{\begin{array} { l } { 1 1 - 2 x \geq 0 } \\{ 2 5 - x ^ { 2 } = 1 2 1 - 4 4 x + 4 x ^ { 2 } }\end{array} \Leftrightarrow \left\{\begin{array} { l } { x \leq \frac { 1 1 } { 2 } } \\{ 5 x ^ { 2 } - 4 4 x + 9 6 = 0 }\end{array} \Leftrightarrow \left\{\begin{array}{l}x \leq \frac{11}{2} \\x=4 \vee x=\frac{24}{5}\end{array} \Leftrightarrow x=4 \vee x=\frac{24}{5} .\right.\right.\right.\end{array}\)Vậy khoảng cách giữa hai điểm \(I, A\) bằng 4 hoặc bằng \(\frac{24}{5}\) thỏa mãn đề bài.
Câu hỏi này nằm trong: