Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của điểm \(A^{\prime}\) lên mặt phẳng \((A B C)\) trùng với trọng tâm của tam giác \(A B C\). Biết khoảng cách giữa hai đường thẳng \(A A^{\prime}\) và \(B C\) bằng \(\frac{a \sqrt{3}}{4}\). Tỉnh theo \(a\) thể tich của khối lẵng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\).
A.
\(V=\frac{a^{3} \sqrt{3}}{24}\).
B.
\(V=\frac{a^{3} \sqrt{3}}{12}\).
C.
\(V=\frac{a^{3} \sqrt{3}}{6}\)
D.
\(V=\frac{a^{3} \sqrt{3}}{3}\).
Giải thích:
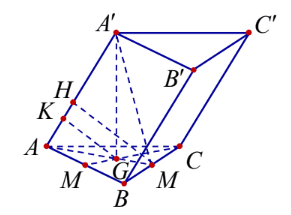
Gọi \(M, G\) lần lượt là trung điểm của \(B C\) và trọng tâm \(G\) của tam giác \(A B C\).
Do tam giác \(A B C\) đều cạnh \(a\) nên \(S_{A S C}=\frac{a^{2} \sqrt{3}}{4}\).
Có: \(\left\{\begin{array}{l}A M \perp B C \\ A^{\prime} G \perp B C\end{array} \Rightarrow B C \perp\left(A A^{\prime} M\right)\right.\).
Trong mặt phẳng \(\left(A A^{\prime} M\right)\) kẻ \(M H \perp A A^{\prime}\).
Khi đó: \(M H \perp B C\) vi \(B C \perp\left(A A^{\prime} M\right)\).
Vậy \(M H\) là đoạn vuông góc chung của \(A A^{\prime}\) và \(B C\) nên \(M H=\frac{a \sqrt{3}}{4}\).
Trong tam giác \(A A^{\prime} G\) kẻ \(G K \perp A H\) thì \(G K / / M H \Rightarrow \frac{G K}{M H}=\frac{A G}{A M}=\frac{2}{3}\).
\(\Rightarrow G K=\frac{2}{3} M H=\frac{2}{3} \cdot \frac{a \sqrt{3}}{4}=\frac{a \sqrt{3}}{6} \text {. }\)Xét tam giác \(A A^{\prime} G\) vuông tại \(G\) ta có: \(\frac{1}{G K^{2}}=\frac{1}{A^{\prime} G^{2}}+\frac{1}{G A^{2}} \Leftrightarrow \frac{1}{\left(\frac{a \sqrt{3}}{6}\right)^{2}}=\frac{1}{A^{\prime} G^{2}}+\frac{1}{\left(\frac{a \sqrt{3}}{3}\right)^{2}}\)
\(\Leftrightarrow \frac{1}{A^{\prime} G^{2}}=\frac{36}{3 a^{2}}-\frac{9}{3 a^{2}}=\frac{9}{a^{2}} \Leftrightarrow A^{\prime} G=\frac{a}{3} \text {. }\)Vậy thể tích của khối lăng trụ đã cho là \(V=A^{\prime} G \cdot S_{A B C}=\frac{a}{3} \frac{a^{2} \sqrt{3}}{4}=\frac{a^{3} \sqrt{3}}{12}\).
Câu hỏi này nằm trong: