Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình chữ nhật, \(A B=a, B C=2 a\). Cạnh bên \(S A=2 a\) và \(S A\) vuông góc với mặt phẳng đáy. Khoáng cách giữa \(S C\) và \(B D\) bằng
A.
\(\frac{2 a}{3}\).
B.
\(\frac{a \sqrt{3}}{2}\).
C.
\(\frac{4 a}{3}\).
D.
\(\frac{3 a}{2}\).
Giải thích:
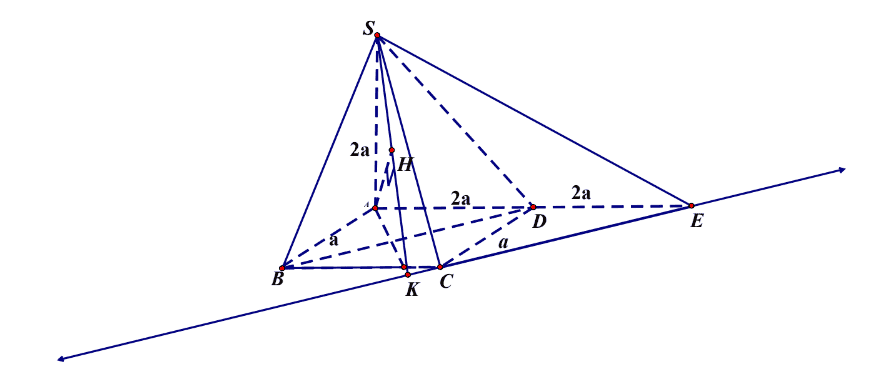
Trong mặt phẳng \((A B C D)\), qua \(\mathrm{C}\) kẻ \(C E / / B D \Rightarrow B D / /(S C E)\)
\(\Rightarrow d(S C, B D)=d(B D,(C S E))=\frac{1}{2} d(A ;(S C E)) \text {. }\)Từ \(A\) kẻ \(A K \perp C E\).
Dễ dàng chứng minh được: \(A H \perp(A C E) \Rightarrow \mathrm{d}(A ;(A C E))=A H\).
+ Tính \(A H\) : Áp dụng hệ thức lượng trong tam giác vuông \(\triangle S A K\)
ta có: \(\frac{1}{A H^{2}}=\frac{1}{S A^{2}}+\frac{1}{A K^{2}}\).
+ Tính \(A K: S_{\triangle C E}=\frac{1}{2} A K \cdot C E=\frac{1}{2} C D \cdot A E \Rightarrow A K=\frac{C D \cdot A E}{C E}=\frac{4 a}{\sqrt{5}}\).
Suy ra:
\(\frac{1}{A H^{2}}=\frac{1}{(2 a)^{2}}+\frac{1}{\left(\frac{4 a}{\sqrt{5}}\right)^{2}}=\frac{9}{16 a^{2}} \Rightarrow A H=\frac{4 a}{3} \Rightarrow \mathrm{d}\left(A ;(S C E)=\frac{4 a}{3} .\right.\)Vây \(d(S C, B D)=\frac{2 a}{3}\).
Câu hỏi này nằm trong: