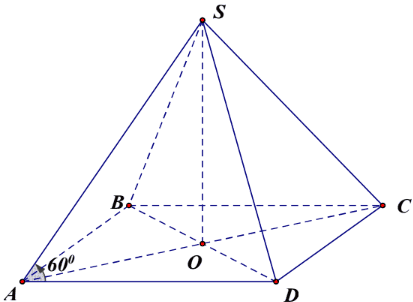
Giả sử ta có hình chóp tứ giác đều \(S . A B C D\).

Gọi \(O\) là giao điểm của \(A C\) và \(B D\). Suy ra \(S O \perp(A B C D)\). Do đó góc giữa cạnh bên \(S A\) và mặt đáy là góc \(\widehat{S A O} \Rightarrow \widehat{S A O}=60^{\circ}\).

Diện tích đáy \(A B C D\) là \(S=a^{2}\).

Ta có \(A C=a \sqrt{2} \Rightarrow A O=\frac{a \sqrt{2}}{2} \Rightarrow S O=A O \cdot \tan \widehat{S A O}=\frac{a \sqrt{2}}{2} \cdot \tan 60^{\circ}=\frac{a \sqrt{6}}{2}\).

Do đó thể tích khối chóp là: \(V=\frac{1}{3} \cdot a^{2} \cdot \frac{a \sqrt{6}}{2}=\frac{a^{3}}{\sqrt{6}}\).