Cho \(\triangle A B C\) đều cạnh \(a\), trực tâm \(H\). Khi đó:
c) \(\overrightarrow{H A}=\overrightarrow{H B}=\overrightarrow{H C}\)
A.
True
B.
False
Giải thích:
Gọi \(M, N\) lần lượt là trung điểm cạnh \(B C, A B\).
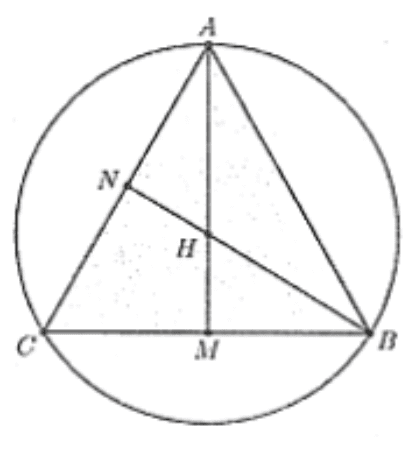
Do tam giác \(A B C\) đều nên \(A M, B N\) cũng là các đường cao của tam giác \(A B C\); vì vậy \(H\) vừa là trực tâm vừa là trọng tâm tam giác này.
Áp dụng định lí Py-tha-go cho \(\triangle A B M\), ta có:
\[\begin{array}{l}A M^{2}=A B^{2}-B M^{2}=a^{2}-\left(\frac{a}{2}\right)^{2}=\frac{3 a^{2}}{4} \\\Rightarrow A M=\frac{a \sqrt{3}}{2} .\end{array}\]Theo tính chất trọng tâm, ta có: \(A H=\frac{2}{3} A M=\frac{2}{3} \cdot \frac{a \sqrt{3}}{2}=\frac{a \sqrt{3}}{3}\).
Dễ thấy ba vectơ \(\overrightarrow{H A}, \overrightarrow{H B}, \overrightarrow{H C}\) có độ dài bằng nhau:
\[|\overrightarrow{H A}|=|\overrightarrow{H B}|=|\overrightarrow{H C}|=A H=\frac{a \sqrt{3}}{3} \text {. }\]Câu hỏi này nằm trong: