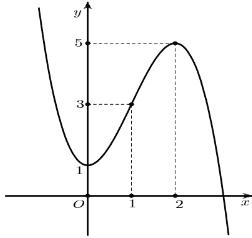
Cho hàm số \(y=f(x)\) là hàm đa thức bậc 4 , có đồ thị hàm số \(y=f^{\prime}(x)\) như hình vẽ. Hàm số \(y=f(5-2 x)+4 x^{2}-10 x\) đồng biến trong các khoảng nào sau đây?
A.
\((3 ; 4)\)
B.
\(\left(2 ; \frac{5}{2}\right)\)
C.
\(\left(\frac{3}{2} ; 2\right)\)
D.
\(\left(0 ; \frac{3}{2}\right)\)
Giải thích:
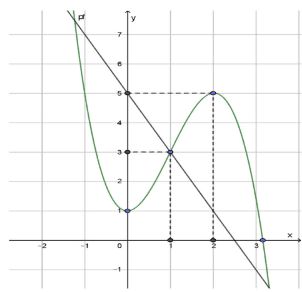
Ta có \(y^{\prime}=-2 f^{\prime}(5-2 x)+8 x-10=-2\left(f^{\prime}(5-2 x)+2(5-2 x)-5\right)\)
Ta có \(y^{\prime} \geq 0 \Leftrightarrow f^{\prime}(5-2 x)+2(5-2 x)-5 \leq 0(*)\). Đặt \(t=5-2 x\) khi đó
\(\left(^{*}\right) \Leftrightarrow f^{\prime}(t)+2 t-5 \leq 0 \Leftrightarrow f^{\prime}(t) \leq-2 t+5\). Từ đồ thị trên ta có:
\(0 \leq t \leq 1 \Leftrightarrow 0 \leq 5-2 x \leq 1 \Leftrightarrow 2 \leq x \leq \frac{5}{2}\)
Câu hỏi này nằm trong: