Cho hình chóp $S . A B C$ có đáy là tam giác đều cạnh 2 . Cạnh bên $S A$ vuông góc với mặt phẳng $(A B C), S A=\sqrt{5}$. Gọi $M$ là trung điể...

Question

Accepted Answer

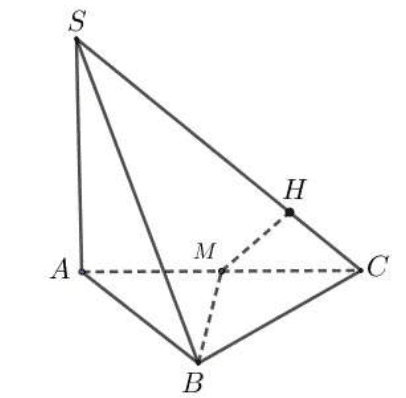
Do tam giác $A B C$ đều nên $B M \perp A C$;

mặt khác $B M \perp S A$ nên $B M \perp(S A C)$.

Trong tam giác $S A C$ dựng $M H \perp S C$.

Vì $B M \perp(S A C)$ nên $B M \perp M H$.

Do đó $M H$ là đoạn vuông góc chung của $B M$ và $S C$ hay $d(B M ; S C)=M H$.

Ta có: $S C=\sqrt{S A^{2}+A C^{2}}=3$.$\triangle S A C$ đồng dạng với $\triangle M H C$ nên

$\frac{S A}{M H}=\frac{S C}{M C} \Leftrightarrow M H=\frac{S A \cdot M C}{S C}=\frac{\sqrt{5} \cdot 1}{3}=\frac{\sqrt{5}}{3}$.

Vậy $d(B M ; S C)=\frac{\sqrt{5}}{3}=\sqrt{\frac{5}{9}}$.

Vậy $a=5, b=9$. Do đó $a+b=14$.