Sắp xếp trước cho 5 nam sinh, số cách hình vẽ): \(C_{6}^{3}\) (cách).

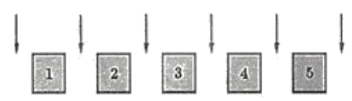
Sắp xếp 3 nữ sinh vào 3 vị trí vừa được chọn: 3 ! (cách).

Vậy số cách xếp hàng thỏa mãn là: \(5!C_{6}^{3} 3!=14400\).

Lưu ý: Việc chọn 3 vị trí thì 6 vị trí để sắp xếp 3 nữ sinh vào có thể được thực hiện gộp bởi công thức \(A_{6}^{3}\). Khi đó số cách xếp thỏa mãn là \(5!A_{6}^{3}\).