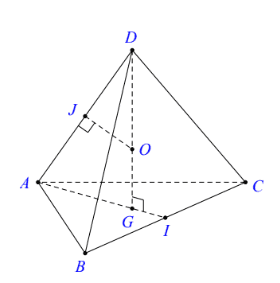
Cho tứ diện \(A B C D\) đều cạnh \(a\).

Gọi \(I\) là trung điểm cạnh \(B C, G\) là trọng tâm của tam giác \(A B C\). Ta có \(A I=\frac{a \sqrt{3}}{2} ; A G=\frac{a \sqrt{3}}{3}\) và \(D G\) là trục của tam giác \(A B C\).

Trong \(\text{mp}(D A G)\) kẻ trung trực cùa \(D A\) cắt \(D G\) tại \(O\) thì \(O D=O A=O B=O C\) nên \(O\) chính là tâm mặt cẩu \((S)\) ngoại tiếp tứ diện \(A B C D\).

Bán kính \(R\) của mặt cầu \((S)\) bằng độ dài đoạn \(O D\).

Trong tam giác \(A D G\) vuông tại \(G\), ta có:\(D A^{2}=D G^{2}+G A^{2} \Rightarrow D G^{2}=D A^{2}-G A^{2}=a^{2}-\left(\frac{a \sqrt{3}}{3}\right)^{2}=\frac{6 a^{2}}{9} \Rightarrow D G=\frac{a \sqrt{6}}{3}\).

Tứ giác \(A G O I\) nội tiếp nên ta có: \(D J \cdot D A=D O \cdot D G \Rightarrow D O=\frac{D A^{2}}{2 D G} \Rightarrow R=D O=\frac{a \sqrt{6}}{4}\).

Diện tích mặt cầu \((S)\) là: \(S=4 \pi R^{2}=4 \pi \cdot\left(\frac{a \sqrt{6}}{4}\right)^{2}=\frac{3 \pi a^{2}}{2}\).