Cho lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có thể tích bằng 324 . Mặt phẳng \((P)\) đi qua trọng tâm \(G\) của tam giác \(A B B^{\prime}\), song song với \(A B^{\prime}\) và \(B C^{\prime}\) chia khối lăng trụ thành hai khối đa diện. Tính thể tích khối đa diện chứa đỉnh \(A\).
Giải thích:
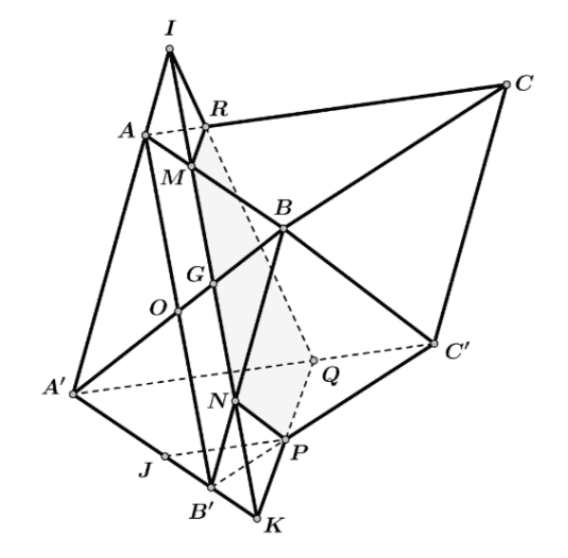
Ta có \(\mathrm{mp}(P)\) đi qua trọng tâm \(G\) của \(\triangle A B B^{\prime}\), song song với \(A B^{\prime}\) và \(B C^{\prime}\) nên cắt lăng trụ theo thiết diện là ngũ giác \(M N P Q R\)
Do \(M N / / A B^{\prime}\) và \(G\) là trọng tâm \(\triangle A B B^{\prime}\) nên
\(\frac{I A}{I A^{\prime}}=\frac{I M}{I K}=\frac{K B^{\prime}}{K A^{\prime}}=\frac{K N}{K I}=\frac{I R}{I Q}=\frac{G O}{G A^{\prime}}=\frac{1}{4}\)\(\Rightarrow \frac{V_{I I A M R}}{V_{I . A^{\prime} K Q}}=\frac{I A}{I A^{\prime}} \cdot \frac{I M}{I K} \cdot \frac{I R}{I Q}=\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}=\frac{1}{64} \Leftrightarrow V_{I . A M R}=\frac{1}{64} V_{I . A^{\prime} K Q}\)- Kẻ \(P J / / A^{\prime} C\) thì \(J P\) là đường trung bình của \(\Delta K A^{\prime} C^{\prime}\) nên \(\frac{K P}{K Q}=\frac{1}{2}\)
\(\Rightarrow \frac{V_{K, B^{\prime} N P}}{V_{K \cdot A^{\prime} I Q}}=\frac{K B^{\prime}}{K A^{\prime}} \cdot \frac{K N}{K I} \cdot \frac{K P}{K Q}=\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{2}=\frac{1}{32} \Leftrightarrow V_{K, B^{\prime} N P}=\frac{1}{32} V_{K . A^{\prime} I Q}\)Khi đó thể tích khối đa diện chứa đỉnh \(A\) là:
\(V=V_{\text {I.AKQ }}-V_{\text {I.AMR }}-V_{K . N P B^{\prime}}=\frac{61}{64} V_{\text {I.AKQ }}\)Mặt khác:
\(\begin{array}{l}V_{I . A^{\prime} K Q}=\frac{1}{3} d\left(I,\left(A^{\prime} K Q\right)\right) \cdot S_{A^{\prime} K Q}=\frac{1}{3} \cdot \frac{4}{3} d\left(A,\left(A^{\prime} K Q\right)\right) \cdot \frac{1}{2} A^{\prime} K \cdot A^{\prime} Q \cdot \sin K A^{\prime} Q \\\Leftrightarrow V_{I . A A^{\prime} K Q}=\frac{1}{3} \cdot \frac{4}{3} d\left(A,\left(A^{\prime} K Q\right)\right) \cdot \frac{1}{2} \cdot \frac{4}{3} A^{\prime} B^{\prime} \cdot \frac{2}{3} A^{\prime} C^{\prime} \cdot \sin K A^{\prime} Q \\\Leftrightarrow V_{\text {I. } A^{\prime} K Q}=\frac{1}{3} \cdot \frac{4}{3} \cdot \frac{4}{3} \cdot \frac{2}{3}\left[\left(\frac{1}{2} A^{\prime} B^{\prime} \cdot A^{\prime} C^{\prime} \cdot \sin K A^{\prime} Q\right) d\left(A,\left(A^{\prime} K Q\right)\right)\right]=\frac{32}{81} V_{A B C \cdot A^{\prime} B^{\prime} C^{\prime}}\end{array}\)Vậy \(V=\frac{61}{64} V_{I . A^{\prime} K Q}=\frac{61}{64} \cdot \frac{32}{81} V_{A B C . A^{\prime} B^{\prime} C^{\prime}}=122\)
Câu hỏi này nằm trong: