Gọi \(z=x+y i,(x, y \in \mathbb{R})\) có biểu diễn hình học là \(M(x ; y)\).

\(\begin{array}{l}\text { +) }|z+\bar{z}+2|+2|z-\bar{z}-2 i| \leq 12 \Leftrightarrow 2|x+1|+4|(y-1) i| \leq 12 \\\Leftrightarrow|x+1|+2|y-1| \leq 6 \text { (1) }\end{array}\)

\(\Rightarrow\) tập hợp điểm \(M\) thỏa mãn \((1)\) thuộc miền trong (tính cả biên) cùa hình thoi \(A B C D\) với \(A(-7 ; 1), B(-1 ;-2), C(5 ; 1), D(-1 ; 4)\) được giới hạn bời bốn đường thẳng \(|x+1|+2|y-1|=6\).

+) \(P=|z-4-4 i|=M I\) với \(I(4 ; 4)\).

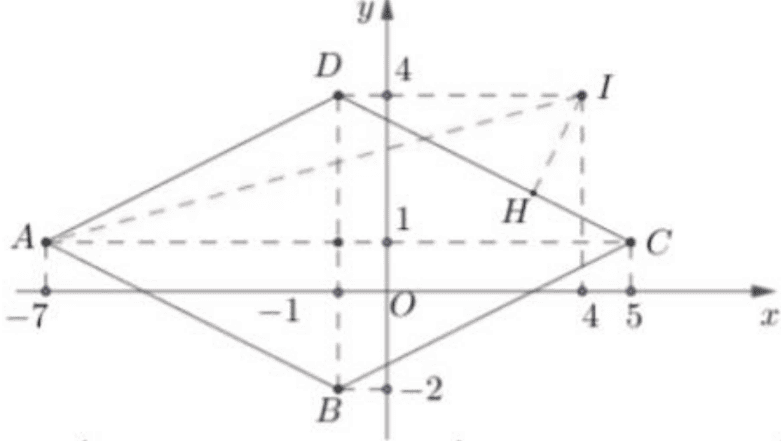
Quan sát hình vẽ, ta thấy: \(P=M I\) đạt giá trị nhỏ nhất khi \(M \equiv H\) là hình chiếu vuông góc của \(I\) lên \(C D: x+2 y-7=0 \Rightarrow m=d(I, C D)=\sqrt{5}\) và \(P=M I\) đạt giá trị lớn nhất khi \(M \equiv A\) khi đó \(M=L A=\sqrt{130}\).

Vậy \(m+M=\sqrt{5}+\sqrt{130}\).