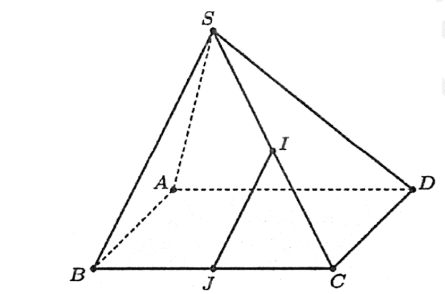
Cho hình chóp \(S \cdot A B C D\) có tất cả các cạnh đều bằng \(a\). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(S C\) và \(B C\). Tìm số đo của góc \((I J, C D)\).
Giải thích:
Tứ giác \(A B C D\) có bốn cạnh bằng nhau nên \(A B C D\) là hình thoi, suy ra \(C D / / A B\).
Ta có \(I J\) là đường trung bình của tam giác \(S B C\) nên \(\left\{\begin{array}{l}I J / / S B \\ I J=\frac{1}{2} S B=\frac{a}{2}\end{array}\right.\).
Do vậy \((I J, C D)=(A B, S B)\).
Mặt khác, tam giác \(S A B\) có ba cạnh bằng nhau nên \(\widehat{S B A}=60^{\circ}\).
Vậy \((I J, C D)=(A B, S B)=\widehat{S B A}=60^{\circ}\).
Câu hỏi này nằm trong: