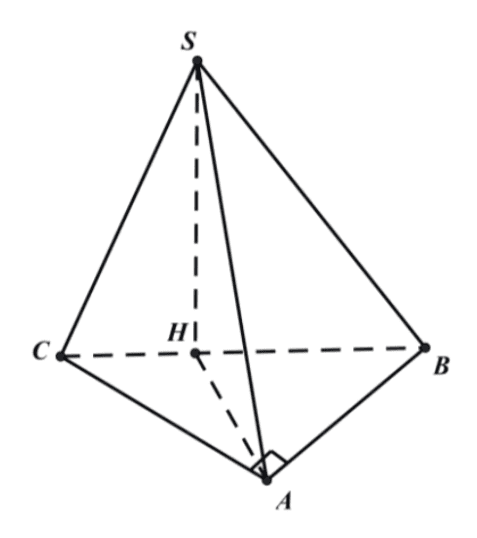
Ta có vì \(S A=S B=S C\) nên \(\Rightarrow S\) nằm trên đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với đáy.

Mà \(\triangle A B C\) vuông cân tại \(A\) nên tâm đường tròn ngoại tiếp đáy là trung điểm \(H\) của \(B C\).

Vậy \(S\) nằm trên đường thẳng đi qua \(H\) vuông góc với \((A B C)\).

Mà góc giữa đường thẳng \(S A\) và \((A B C)\) là \(60^{\circ} \Rightarrow S A H=60^{\circ}\)\(\triangle A B C\) vuông cân tại A có \(A B=2 a \Rightarrow \Rightarrow B C=2 a \sqrt{2}\).

Mà \(H\) là trung điểm của \(B C \Rightarrow A H=\frac{1}{2} B C=a \sqrt{2}\)

Xét tam giác vuông \(S H A\) ta có: \(S H=A H \cdot \tan 60^{\circ}=a \sqrt{6} \xrightarrow{a=\sqrt{6}} S H=6\)

Vậy khoảng cách từ \(S\) đến đường thẳng \(B C\) là 6 .