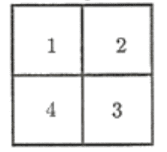
Một quán cafe nhạc cần trang trí một bức tường vuông được chia thành bốn ô như hình vẽ. Có bao nhiêu cách để người thợ sơn có thể dùng bốn màu khác nhau để sơn tấm tường này sao cho mỗi ô vuông được tô một màu và những ô vuông cạnh nhau không có màu trùng nhau?
Giải thích:
Trường hợp 1. ô số 1 và ô số 3 cùng màu.
Chọn màu cho ô số 1: có 4 cách. Chọn màu cho ô số 3: có 1 cách.
Hai ô số 2 và 4 đều có cùng số cách chọn là 3 .
Vậy số cách chọn màu trong trường hợp này là: \(4 \times 1 \times 3 \times 3=36\).
Trường hợp 2: Ô số 1 và ô số 3 không cùng màu.
Chọn màu cho ô số 1: có 4 cách. Chọn màu cho ô số 3 : có 3 cách.
Hai ô số 2 và 4 đều có cùng số cách chọn là 2 .
Vậy số cách chọn màu trong trường hợp này là: \(4 \times 3 \times 2 \times 2=48\).
Vậy số cách chọn màu thỏa mãn là: \(36+48=84\).
Câu hỏi này nằm trong: