Cho khối tứ diện \(A B C D\). Gọi \(M, N\) lần lượt là trung điểm của các cạnh \(A B, C D ; P\) là điểm nằm trong đoạn \(B C\) sao cho \(B P=k P C(k\gt 1)\).
a) Tính thể tích khối tứ diện \(A B C D\) trong trường hợp \(\triangle A C D\) vuông tại \(A, \triangle B C D\) vuông cân tại \(B\) và \(A B=A C=A D=a\).
Giải thích:
Vẽ hình
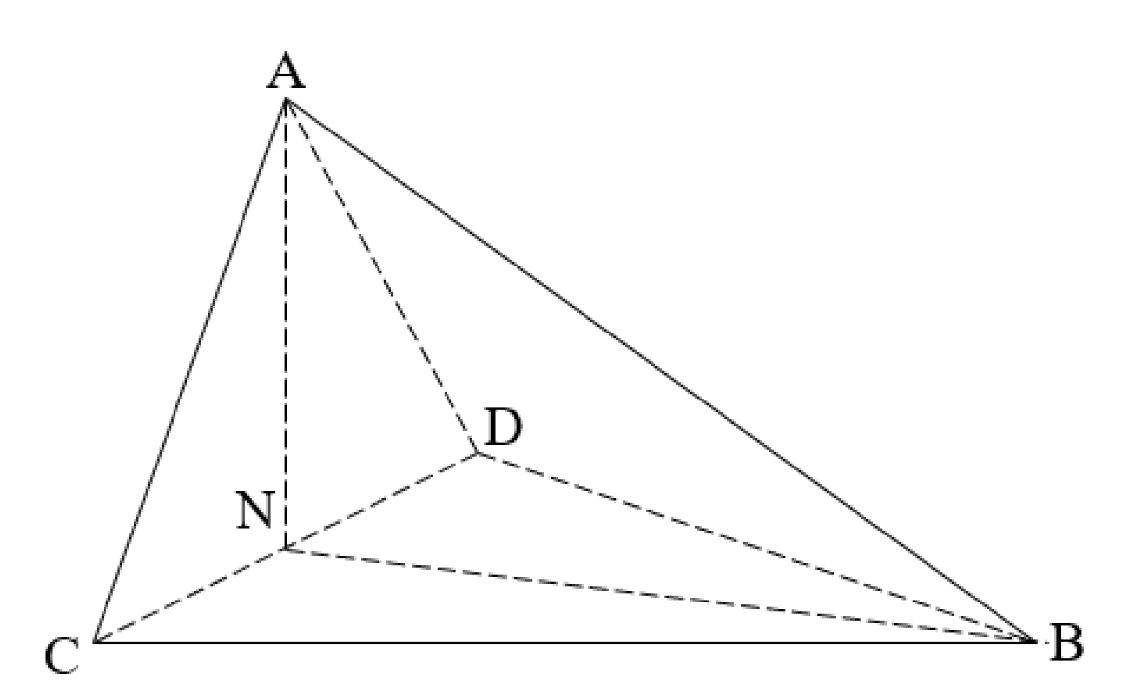
Có \(N\) là trung điểm của \(C D\)
\(\triangle B C D\) vuông cân tại \(B \Rightarrow N\) là tâm đường tròn ngoại tiếp \(\triangle B C D\) và \(B N=\frac{C D}{2}=\frac{a \sqrt{2}}{2}\)
Lại có \(A B=A C=A D=a \Rightarrow A N \perp(B C D)\) và \(A N=\frac{C D}{2}=\frac{a \sqrt{2}}{2}\)
\(S_{\triangle B C D}=\frac{1}{2} B N \cdot C D=\frac{C D^{2}}{4}=\frac{a^{2}}{2}\)Vậy \(V_{A B C D}=\frac{1}{3} A N \cdot S_{\triangle B C D}=\frac{a^{3} \sqrt{2}}{12}\).
Câu hỏi này nằm trong: