Hai chất điểm \(\mathrm{A}, \mathrm{C}\) chuyền động thẳng đều trên hai đường thẳng tạo với nhau một góc \(\alpha=30^{\circ}\) với tốc độ tương ứng \(\mathrm{v}_{1}, \mathrm{v}_{2}\) (với \(\mathrm{v}_{2}=\frac{\mathrm{v}_{1} \sqrt{3}}{3}\) ) và đang hướng về phía giao điểm \(\mathrm{B}\) (như hình vẽ). Tại thời điểm khoảng cách giữa hai chất điểm đạt giá trị nhỏ nhất thì chất điểm \(\mathrm{A}\) cách giao điểm \(\mathrm{B}\) một đoạn \(\mathrm{d}_{1}=30 \sqrt{3} \mathrm{~m}\), khi đó chất điểm C cách giao điểm B một đoạn bao nhiêu.
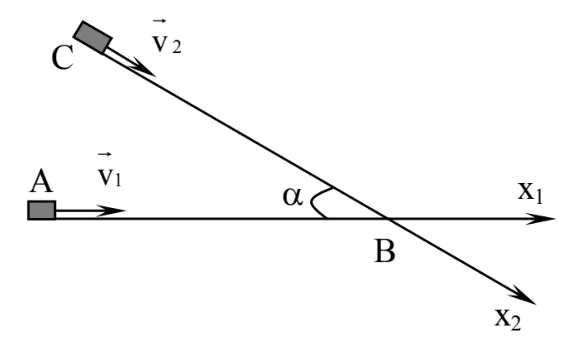
Giải thích:
+ Gọi d1, d2 là khoảng cách từ vật 1 và vật 2 đến O lúc đầu ta xét (t = 0 ).
+ Áp dụng định lý hàm sin ta có:
+ Áp dụng tính chất của phân thức ta có:
\(\begin{array}{l}\frac{\mathrm{d}_{1}-\mathrm{v}_{1} \mathrm{t}}{\sin \gamma}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{v}_{1} \mathrm{t}}{\sqrt{3} \sin \beta}=\frac{\left(\sqrt{3} \mathrm{~d}_{2}-\mathrm{v}_{1} \mathrm{t}\right)-\left(\mathrm{d}_{1}-\mathrm{v}_{1} \mathrm{t}\right)}{\sqrt{3} \sin \beta-\sin \gamma}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\sqrt{3} \sin \beta-\sin \gamma} \\\Rightarrow \frac{\mathrm{d}}{\sin 30^{\circ}}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\sqrt{3} \sin \beta-\sin \gamma}\end{array}\)+ Mặt khác, tacó: \(\sin \beta=\sin \left(180^{\circ}-\beta\right)=\sin (\alpha+\gamma)=\sin \left(30^{\circ}+\gamma\right)\)
\(\Rightarrow \sqrt{3} \sin \beta=\sqrt{3} \sin \left(30^{\circ}+\gamma\right)=\sqrt{3}\left(\sin 30^{\circ} \cos \gamma+\cos 30^{\circ} \sin \gamma\right) \Rightarrow \sqrt{3} \sin \beta=\frac{\sqrt{3}}{2} \cos \gamma+\frac{3}{2} \sin \gamma\)(2)+ Thay (2) vào (1) ta có:
\(\frac{\mathrm{d}}{\sin 30^{\circ}}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\frac{\sqrt{3}}{2} \cos \gamma+\frac{3}{2} \sin \gamma-\sin \gamma} \Rightarrow d=\frac{\left(\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}\right) \sin 30^{\circ}}{\frac{\sqrt{3}}{2} \cos \gamma+\frac{1}{2} \sin \gamma}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\sqrt{3} \cos \gamma+\sin \gamma}\)+ Vậy \(\mathrm{d}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\sqrt{3} \cos \gamma+\sin \gamma}=\frac{\sqrt{3} \mathrm{~d}_{2}-\mathrm{d}_{1}}{\mathrm{y}}\)+ Khoảng cách giữa hai vật \(\mathrm{d}_{\min } \Leftrightarrow \mathrm{y}_{\max }\) với \(\mathrm{y}=\sqrt{(\sqrt{3} \cos \gamma+\sin \gamma)^{2}}\)+ Áp dụng bất đẳng thức Bunhia Côpski:
\(\sqrt{(\sqrt{3} \cos \gamma+\sin \gamma)^{2}} \leq \sqrt{\left[(\sqrt{3})^{2}+1^{2}\right] \cdot\left[\cos ^{2} \gamma+\sin ^{2} \gamma\right]}=2 \Rightarrow \mathrm{y}_{\max }=2\)Dấu "=" xảy ra khi và chỉ khi \(\sqrt{3} \cos \gamma=\sin \gamma \Leftrightarrow \frac{\sqrt{3}}{1}=\frac{\cos \gamma}{\sin \gamma} \Rightarrow \tan \gamma=\frac{1}{\sqrt{3}} \Rightarrow \gamma=30^{\circ}\) và \(\beta=120^{\circ}\)
\(\text { + Lúc đó: } \frac{\mathrm{d}_{1}^{\prime}}{\sin 30^{\circ}}=\frac{\mathrm{d}_{2}^{\prime}}{\sin 120^{\circ}} \Rightarrow \mathrm{d}_{2}^{\prime}=\frac{\sin 120^{\circ}}{\sin 30^{\circ}} \cdot \mathrm{d}_{1}^{\prime}=\sqrt{3} \mathrm{~d}_{1}^{\prime}=90(\mathrm{~m})\)+ Vậy, khoảng cách từ vật hai đến \(\mathrm{O}\) lúc này là: \(\mathrm{d}_{2}^{\prime}=90(\mathrm{~m})\)
Câu hỏi này nằm trong: