Tổng các nghiệm nguyên của bất phương trình \(2 x^{2}-5 x+2 \leq 0\) là:
A.
3
B.
4
C.
5
D.
6
Giải thích:
Đặt \(f(x)=2 x^{2}-5 x+2\).
Ta có: \(2 x^{2}-5 x+2=0 \Leftrightarrow\left[\begin{array}{l}x=\frac{1}{2} \\ x=2\end{array}\right.\).
Trục xét dấu \(f(x)\)
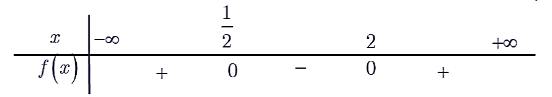
Do đó: \(2 x^{2}-5 x+2 \leq 0 \Leftrightarrow x \in\left[\frac{1}{2} ; 2\right]\).
Vậy các nghiệm nguyên của bất phương trình trên là: \(x=1 ; x=2\).
Suy ra tổng các nghiệm nguyên của bất phương trình trên là 3 .
Câu hỏi này nằm trong: