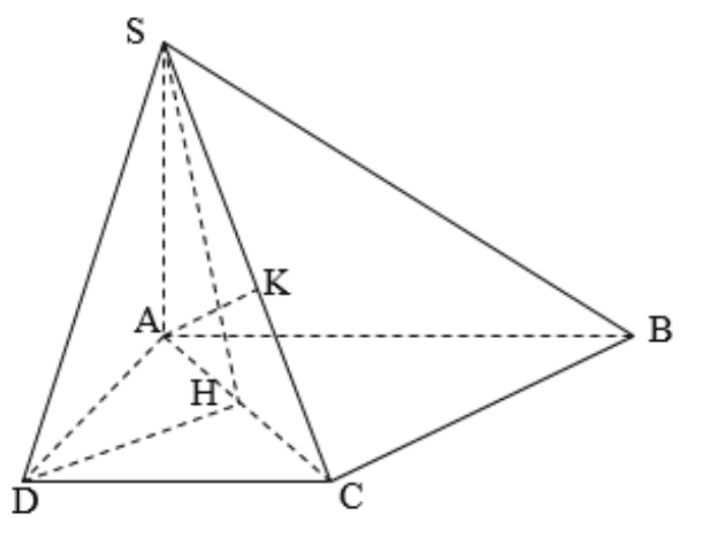
Vì \(A B C D\) là hình thanh vuông tại \(A\) và \(D, A B=2 A D=2 C D=2 a\) nên ta có \(d(D,(S B C))=\frac{1}{2} d(A,(S B C))\).

Kẻ \(A K \perp S C\) tại \(K\). 

Theo chứng minh ý b) ta có \(B C \perp(S A C)\) nên \(A K \perp B C\), do đó \(A K \perp(S B C)\).

Xét tam giác \(S A C\) vuông tại \(A\) có \(S A=2 a, A C=a \sqrt{2}\) suy ra \(A K=\frac{2 a \sqrt{3}}{3}\).

Vậy \(d(D,(S B C))=\frac{1}{2} d(A,(S B C))=\frac{1}{2} A K=\frac{a \sqrt{3}}{3}\). Mệnh đề đúng.