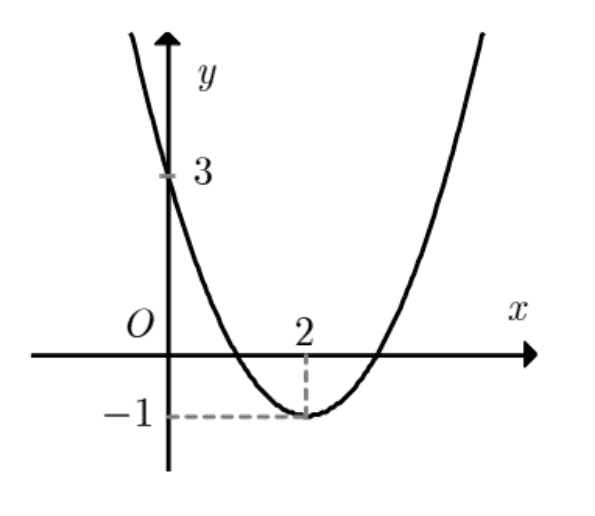
Cho hàm số \(f(x)=a x^{2}+b x+c\) đồ thị như hình bên. Tìm tất cả các giá trị của tham số thực \(\mathrm{m}\) để phương trình \(f(|x|)-1=m\) có đúng 3 nghiệm phân biệt.
Giải thích:
Ta có \(f(|x|)=f(x)\) nếu \(x \geq 0\). Hơn nữa hàm \(f(|x|)\) là hàm số chẵn. Từ đó suy ra cách vẽ đồ thị hàm số \((C)\) từ đồ thị hàm số \(y=f(x)\) như sau:
- Giữ nguyên đồ thị \(y=f(x)\) phía bên phải trục tung.
- Lấy đối xứng phần đồ thị \(y=f(x)\) phía bên phải trục tung qua trục tung.
Kết hợp hai phần ta được đồ thị hàm số \(y=|f(x)|\) như hình vẽ.
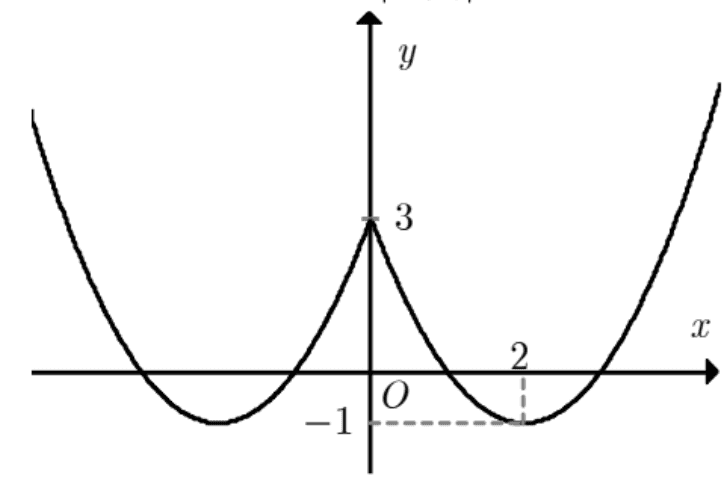
Phương trình \(f(|x|)-1=m \Leftrightarrow f(|x|)=m+1\) là phương trình hoành độ giao điểm của đồ thị hàm số \(y=f(|x|)\) và đường thẳng \(y=m+1\) (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt khi và chỉ \(\mathrm{m}=2\)
Câu hỏi này nằm trong: