Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình vuông có tâm \(O\). Cạnh bên \(S A\) vuông góc với đáy \(A B C D, H\) là hình chiếu vuông góc của \(A\) trên \(S O\). Khi đó:
c) \(C D \perp(S A D)\)
A.
B.
Giải thích:
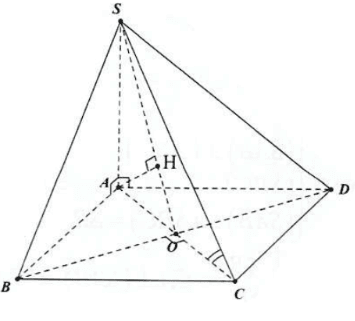
\(\begin{array}{l}\left\{\begin{array}{l}B D \perp A C \\ B D \perp S A(S A \perp(A B C D))\end{array} \Rightarrow B D \perp(S A C)\right. \\ \left\{\begin{array}{l}B D \perp(S A C) \\ S C \subset(S A C)\end{array} \Rightarrow B D \perp S C\right. \\ \left\{\begin{array}{l}C D \perp A D \\ C D \perp S A\end{array} \Rightarrow C D \perp(S A D)\right. \\ \left\{\begin{array}{l}A H \perp S O \\ A H \perp B D(B D \perp(S A C))\end{array} \Rightarrow A H \perp(S B D) \Rightarrow A H \perp S B\right.\end{array}\)
Câu hỏi này nằm trong: