Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có độ dài cạnh bằng \(10 \). Tính khoảng cách giữa hai mặt phẳng \(\left(A D D^{\prime} A^{\prime}\right)\) và \(\left(B C C^{\prime} B^{\prime}\right)\).
A.
\(\sqrt{10}\)
B.
\(100\)
C.
\(10\)
D.
\(5\)
Giải thích:
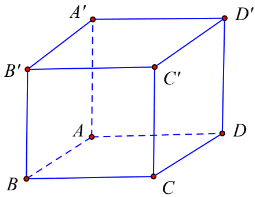
Ta có \(\left(A D D^{\prime} A^{\prime}\right) / /\left(B C C^{\prime} B^{\prime}\right) \Rightarrow d\left(\left(A D D^{\prime} A^{\prime}\right) ;\left(B C C^{\prime} B^{\prime}\right)\right)=d\left(A ;\left(\left(B C C^{\prime} B^{\prime}\right)\right)\right)\) \(=AB=10\)
Câu hỏi này nằm trong: