Cho hình chóp \(S . A B C\) có \(A B C\) là tam giác đều cạnh \(a\) và cạnh bên \(S A\) vuông góc với đáy, với \(S A=\frac{a}{2}\).
d) Gọi \(P, Q\) lần lượt là trung điểm \(S B, S C\). Thể tích khối chóp \(A \cdot B C Q P\) bằng \(\frac{a^{3} \sqrt{3}}{12}\)
A.
True
B.
False
Giải thích:
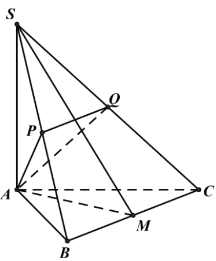
Sai: Ta có: \(\frac{V_{S . A P Q}}{V_{S . A B C}}=\frac{S A}{S A} \cdot \frac{S P}{S B} \cdot \frac{S Q}{S C}=1 \cdot \frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4}\)
Suy ra \(V_{S . A P Q}=\frac{1}{4} V_{S . A B C}=\frac{1}{4} \cdot \frac{a^{3} \sqrt{3}}{24}=\frac{a^{3} \sqrt{3}}{96}\)
Do đó: \(V_{A . B C Q P}=V_{S . A B C}-V_{S . A P Q}=\frac{a^{3} \sqrt{3}}{24}-\frac{a^{3} \sqrt{3}}{96}=\frac{a^{3} \sqrt{3}}{32}\)
Câu hỏi này nằm trong: