Cho hình chóp \(\mathrm{S} . \mathrm{ABCD}\) có đáy ABCD là hình vuông cạnh \(\mathrm{a}, \mathrm{SA} \perp(\mathrm{ABCD}), \mathrm{SA}=\mathrm{x}\). Tìm x để hai mặt phẳng \((\mathrm{SBC})\) và \((\mathrm{SCD})\) tạo với nhau một góc \(60^{\circ}\) :
A.
\(x=\frac{3 a}{2}\)..
B.
\(\mathrm{x}=2 \mathrm{a}\).
C.
\(x=\frac{a}{2}\).
D.
\(x=a\)
Giải thích:
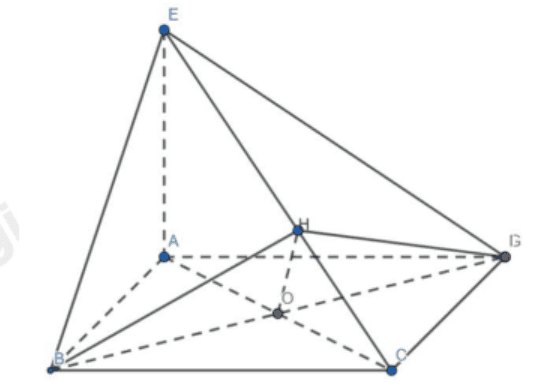
Kẻ \(B H \perp S C \Rightarrow D H \perp S C\) (hai đường cao tương ứng của hai tam giác bằng nhau)
\(\Rightarrow((S B C),(S C D))=(B H, D H)=60^{\circ}\)
Có hai trường hợp xảy ra:
TH1:
\(\begin{array}{l}\widehat{B H D}=60^{\circ} \Rightarrow \widehat{B H O}=30^{\circ} \\O B=\frac{a}{\sqrt{2}}, \tan 30^{\circ}=\frac{O B}{O H} \Rightarrow O H=\frac{\frac{a}{\sqrt{2}}}{\frac{1}{\sqrt{3}}}=a \sqrt{\frac{3}{2}}\end{array}\)Xét hai tam giác đồng dạng \(S A C\) và \(O H C\) ta có:
\(\begin{array}{l}\frac{O H}{O C}=\frac{S A}{S C} \Leftrightarrow \frac{a \sqrt{\frac{3}{2}}}{\frac{a}{\sqrt{2}}}=\frac{x}{\sqrt{x^{2}+2 a^{2}}} \Leftrightarrow \sqrt{3}=\frac{x}{\sqrt{x^{2}+2 a^{2}}} \Leftrightarrow 3\left(x^{2}+2 a^{2}\right)= \\\Leftrightarrow 2 x^{2}+6 a^{2}=0\end{array}\)\(\Leftrightarrow x=a \sqrt{3}\) (không có đáp án nào thỏa mãn)
TH2:
\(\begin{array}{l}\widehat{B H D}=120^{\circ} \Rightarrow \widehat{B H O}=60^{\circ} \\O B=\frac{a}{\sqrt{2}}, \tan 60^{\circ}=\frac{O B}{O H} \Rightarrow O H=\frac{\frac{a}{\sqrt{2}}}{\sqrt{3}}=\frac{a}{\sqrt{6}}\end{array}\)Xét hai tam giác đồng dạng \(S A C\) và \(O H C\) ta có:
\(\begin{array}{l}\frac{O H}{O C}=\frac{S A}{S C} \Leftrightarrow \frac{\frac{a}{\sqrt{6}}}{\frac{a}{\sqrt{2}}}=\frac{x}{\sqrt{x^{2}+2 a^{2}}} \Leftrightarrow \frac{1}{\sqrt{3}}=\frac{x}{\sqrt{x^{2}+2 a^{2}}} \Leftrightarrow x^{2}+2 a^{2}=3 x^{2} \\\Leftrightarrow x=a\end{array}\)Câu hỏi này nằm trong: