Cho hình chóp \(S . A B C D\) có \(S A\) vuông góc với mặt phẳng \((A B C D), A B C D\) là hình thang vuông có đáy lớn \(A D\) gấp đôi đáy nhỏ \(B C\), đồng thời đường cao \(A B=B C=a\). Biết \(S A=a \sqrt{3}\), khi đó khoảng cách từ đình \(B\) đến đường thẳng \(S C\) là.
A.
\(a \sqrt{10}\)
B.
\(2 a\).
C.
\(\frac{2 a \sqrt{5}}{5}\)
D.
\(\frac{a \sqrt{10}}{5}\).
Giải thích:
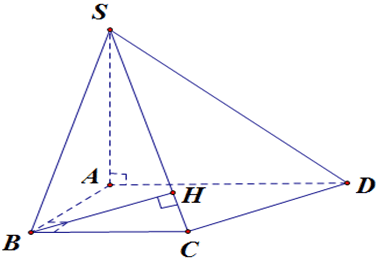
Ta có: \(\left\{\begin{array}{l}B C \perp A B \\ B C \perp S A\end{array} \Rightarrow B C \perp S B \Rightarrow \triangle S B C\right.\) vuông tại \(B\).
Trong \(\triangle S B C\) dựng đường cao \(B H \Rightarrow d(B ; S C)=B H\).
\(S B=2 a ; \frac{1}{B H^{2}}=\frac{1}{S B^{2}}+\frac{1}{B C^{2}} \Rightarrow B H=\frac{B S \cdot B C}{\sqrt{B S^{2}+B C^{2}}}=\frac{2 a \sqrt{5}}{5}\)Câu hỏi này nằm trong: