Số các giá trị nguyên nhỏ hơn 2020 của tham số \(m\) để phương trình \(\log _{6}(2020 x+m)=\log _{4}(1010 x)\) có nghiệm là
A.
2022 .
B.
2020 .
C.
2019 .
D.
2021 .
Giải thích:
Ta đặt \(\log _{6}(2020 x+m)=\log _{4}(1010 x)=t\).
Khi đó \(2020 x+m=6^{t}\) và \(1010 x=4^{t}\).
Ta suy ra \(2 \cdot 4^{t}+m=6^{t} \Leftrightarrow m=6^{t}-2 \cdot 4^{t}\)
Đặt \(f(t)=-2.4^{t}+6^{t}\)
\(\begin{array}{l}f^{\prime}(t)=6^{\prime} \ln 6-2 \cdot 4^{\prime} \cdot \ln 4 \\f^{\prime}(t)=0 \Rightarrow\left(\frac{3}{2}\right)^{t}=\frac{2 \ln 4}{\ln 6}=\log _{6} 16 \Leftrightarrow t=\log _{\frac{3}{2}}\left(\log _{6} 16\right) .\end{array}\)Bảng biến thiên
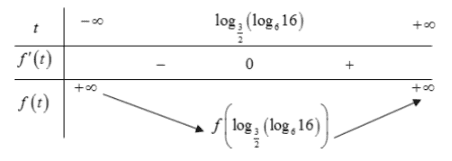
Phương trình \(f(t)=m\) có nghiệm khi và chi khi \(m \geq f\left(\log _{\frac{3}{2}}\left(\log _{6} 16\right)\right) \approx-2,01\).
Hơn nữa, \(\left\{\begin{array}{l}m\lt 2020 \\ m \in \mathbb{Z}\end{array}\right.\) nên suy ra \(\left\{\begin{array}{l}-2 \leq m \leq 2019 \\ m \in \mathbb{Z}\end{array}\right.\).
Vậy ta có 2022 giá trị \(m\) thỏa mãn.
Câu hỏi này nằm trong: